题目内容
1.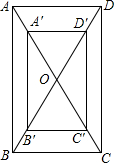 一个矩形的广告牌如图所示,印刷厂的纸张的印刷面积是32dm2,上、下空白各1dm,左、右空白处各0.5dm,被印刷部分从上到下的长是xdm,四周空白处的面积为Sdm2.
一个矩形的广告牌如图所示,印刷厂的纸张的印刷面积是32dm2,上、下空白各1dm,左、右空白处各0.5dm,被印刷部分从上到下的长是xdm,四周空白处的面积为Sdm2.(1)求S与x之间的关系式.
(2)若要求四周空白处的面积为18dm2,求用来印刷广告的纸张的长和宽的各是多少?
(3)在(2)的条件下,内外两个矩形是位似图形吗?说明理由.
分析 (1)先表示出AB=x+2,A′D′=$\frac{32}{x}$,AD=$\frac{32}{x}$+1,则利用S=S矩形ABCD-S矩形A′B′C′D′可得S=$\frac{64}{x}$+x+2;
(2)解方程$\frac{64}{x}$+x+2=18得x1=x2=8,经检验x=8是原方程的解,然后计算$\frac{32}{x}$,从而得到用来印刷这张广告的纸张的长和宽;
(3)先计算$\frac{A′B′}{AB}$=$\frac{8}{10}$=$\frac{4}{5}$,$\frac{A′D′}{AD}$=$\frac{4}{5}$,所以$\frac{A′B′}{AB}$=$\frac{A′D′}{AD}$=$\frac{A′C′}{AC}$=$\frac{B′C′}{BC}$,加上所有对应角为直角,根据位似图形的判定方法可判断内外两个矩形是位似图形.
解答 解:(1)根据题意得A′B′=x,则AB=x+2,A′D′=$\frac{32}{x}$,
所以AD=$\frac{32}{x}$+1,
所以S=S矩形ABCD-S矩形A′B′C′D′=(x+2)•($\frac{32}{x}$+1)-32=$\frac{64}{x}$+x+2,
(2)当S=18,即$\frac{64}{x}$+x+2=18,
整理得x2-16x+64=0,解得x1=x2=8,
经检验x=8是原方程的解,
则$\frac{32}{x}$=4,
所以用来印刷这张广告的纸张的长和宽各是8dm,4dm;
(3)内外两个矩形是位似图形.理由如下:
因为$\frac{A′B′}{AB}$=$\frac{8}{10}$=$\frac{4}{5}$,$\frac{A′D′}{AD}$=$\frac{4}{5}$,
所以$\frac{A′B′}{AB}$=$\frac{A′D′}{AD}$=$\frac{A′C′}{AC}$=$\frac{B′C′}{BC}$,
所以内外两个矩形是位似图形.
点评 本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.也考查了一元二次方程的应用.

| A. | -1 | B. | 0 | C. | 1 | D. | 10 |
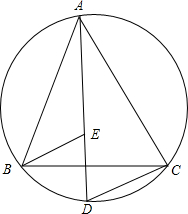 如图,△ABC的顶点A,B,C都在圆上,$\widehat{AB}$=$\widehat{BC}$=$\widehat{AC}$,D是$\widehat{BC}$上一点,连接AD,在AD上截取AE=DC,试判断△BDE的形状,并说明理由.
如图,△ABC的顶点A,B,C都在圆上,$\widehat{AB}$=$\widehat{BC}$=$\widehat{AC}$,D是$\widehat{BC}$上一点,连接AD,在AD上截取AE=DC,试判断△BDE的形状,并说明理由.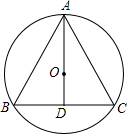 ⊙0外接等腰△ABC,AB=AC,连AO并延长BC与D,BC=12,cosB=$\frac{3}{5}$,求:半径长.
⊙0外接等腰△ABC,AB=AC,连AO并延长BC与D,BC=12,cosB=$\frac{3}{5}$,求:半径长.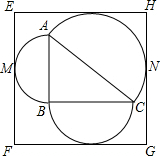 如图,在Rt△ABC中,∠B=90°,以其三边为直径向三角形外作三个半圆,正方形EFGH的各边分别与半圆相切且平行于AB或BC.如果正方形EFGH的面积是144cm2,则Rt△ABC的周长是24cm.
如图,在Rt△ABC中,∠B=90°,以其三边为直径向三角形外作三个半圆,正方形EFGH的各边分别与半圆相切且平行于AB或BC.如果正方形EFGH的面积是144cm2,则Rt△ABC的周长是24cm.