题目内容
14．
如图，在△ABC中，∠B=90°，AB=9cm，点P从点A开始沿AB方向以1cm/s的速度移动，点Q从点B开始沿BC方向以2cm/s的速度移动，如果点P，Q分别从点A，B同时出发，几秒后△PQB为等腰三角形？
分析 首先设x秒后△PQB为等腰三角形，则根据题意得：AP=xcm，BQ=2xcm，可得当BP=BQ时，△PQB为等腰三角形，即9-x=2x，解此方程即可求得答案．
解答 解：设x秒后△PQB为等腰三角形，
根据题意得：AP=xcm，BQ=2xcm，
则BP=AB-AP=9-x（cm），
∵在△ABC中，∠B=90°，
∴当BP=BQ时，△PQB为等腰三角形，
即9-x=2x，
解得：x=3，
∴3秒后△PQB为等腰三角形．
点评 此题考查了等腰三角形的判定．首先设x秒后△PQB为等腰三角形，然后结合题意表示出各线段的长是关键．
练习册系列答案
名校课堂系列答案
相关题目
5．已知⊙O1与⊙O2相交，且两圆的半径分别为2cm和3cm，则圆心距O1O2可能是（ ）
| A． | 1cm | B． | 3cm | C． | 5cm | D． | 7cm |
2．计算（$\frac{2}{3}$）2014×1.52015×（-1）2016的结果是（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{3}{2}$ | C． | -$\frac{2}{3}$ | D． | -$\frac{3}{2}$ |
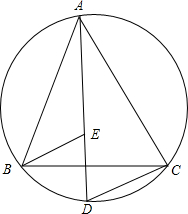如图，△ABC的顶点A，B，C都在圆上，$\widehat{AB}$=$\widehat{BC}$=$\widehat{AC}$，D是$\widehat{BC}$上一点，连接AD，在AD上截取AE=DC，试判断△BDE的形状，并说明理由．
已知正三角形的边长为a，求它的内切圆与外接圆所围成的圆环的面积．
6．若a=$\sqrt{5}$，b=$\root{3}{5}$，则a2-b3的值是（ ）
| A． | -1 | B． | 0 | C． | 1 | D． | 10 |
若二次函数y=ax2+bx+a2-1（a≠0）的图象如图所示，则a的值是-1．