题目内容
4.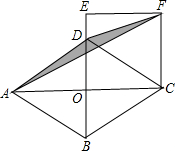 如图,在菱形ABCD中,对角线AC,BD长分别为8和6,延长OD到E,使OE=OC,以OE为边构造正方形OEFC,连接DF,AF,则△ADF的面积是( )
如图,在菱形ABCD中,对角线AC,BD长分别为8和6,延长OD到E,使OE=OC,以OE为边构造正方形OEFC,连接DF,AF,则△ADF的面积是( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 设OE与AF相交于点M,由正方形性质可得OM∥CF,进而可证明△AOM∽△ACF,由相似三角形的性质可求出OM的长,所以DM也可求出,再利用三角形面积公式即可求出△ADF的面积.
解答 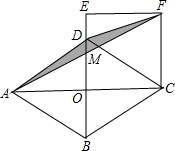 解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,
∴AO=OC,OD=OB,BD⊥AC,
∵AC=8,BD=6,
∴AO=OC=4,DO=BO=3,
∵四边形OEFC是正方形,
∴OE=OC=CF=EF=3,OM∥CF,
∴△AOM∽△ACF,
∴OM:CF=AO:AC,
即OM:3=4:8,
解得OM=1.5,
∴DM=OD-OM=0.5,
∴△ADF的面积=$\frac{1}{2}$DM•AO+$\frac{1}{2}$DM•EF=$\frac{1}{2}$×0.5×4+$\frac{1}{2}$×0.5×4=2,
故选A.
点评 本题考查了菱形的性质、正方形的性质、相似三角形的判定和性质以及三角形面积公式的运用,题目的综合性较强,难度中等,解题的关键是正确求出DM的长.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 根据图中标示的数据,计算图形的周长(单位:mm)
根据图中标示的数据,计算图形的周长(单位:mm)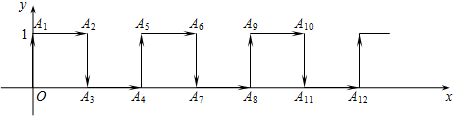
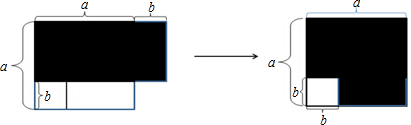
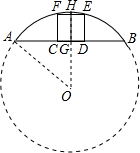 如图,四边形CDEF是弓形的内接正方形,已知弓形的弦AB长为8,弓形的高HG为2.
如图,四边形CDEF是弓形的内接正方形,已知弓形的弦AB长为8,弓形的高HG为2.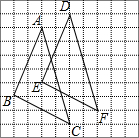 如图,每个小正方形的边长为1,三角形ABC的三个顶点都在格点(小正方形的顶点)上,
如图,每个小正方形的边长为1,三角形ABC的三个顶点都在格点(小正方形的顶点)上, 如图,BD是△ABC的高,AE是△ABC的角平分线,BD交AE于F,若∠BAC=44°,∠C=80°,求∠BEF和∠AFD的度数.
如图,BD是△ABC的高,AE是△ABC的角平分线,BD交AE于F,若∠BAC=44°,∠C=80°,求∠BEF和∠AFD的度数.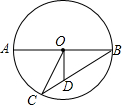 如图,半径为5的⊙O中,AB是直径,弦BC=8,OD⊥AB交BC于D,求CD的长及△OCD的面积.
如图,半径为5的⊙O中,AB是直径,弦BC=8,OD⊥AB交BC于D,求CD的长及△OCD的面积.