题目内容
13．
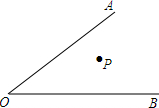已知，如图所示，甲、乙、丙三个人做传球游戏，游戏规则如下：甲将球传给乙，乙将球立刻传给丙，然后丙又立刻将球传给甲．若甲站在角AOB内的P点，乙站在OA上，丙站在OB上，并且甲、乙、丙三人的传球速度相同．问乙和丙必须站在何处，才能使球从甲到乙、乙到丙、最后丙到甲这一轮所用的时间最少？请作图说明（保留作图痕迹，不写作法）．
分析 欲求一轮所用的时间最少，即使得三者传球的距离最短，分别作P点关于OA、OB的对称点P2、P1，连接P2、P1交OA于D，交OB于点Q，D就是乙所处的位置，Q点就是丙所在的位置．
解答 解：如图：
D就是乙所处的位置，Q点就是丙所在的位置．
点评 此题主要考查了轴对称最短路径问题，关键是确定丙，乙的位置．
练习册系列答案
相关题目
如图所示，在平行四边形ABCD中，∠BAD的平分线AE交CD于E，若∠DAE=35°，求∠C与∠B的度数．
4．数据4、5、7、8、6、13、5的中位数是（ ）
| A． | 5 | B． | 6 | C． | 7 | D． | 8 |
如图，△AOB是等腰直角三角形，AO=AB，∠OAB=90°，C为OB上任意一点，以AC为直角边作等腰直角三角形ACD，∠ACD=90°．连接OD，求∠AOD的度数．
18．有一条东西走向的公路，一辆汽车从A地出发向东行驶18千米到达B地，又从B地返回向西行驶20千米到达C地，设从西向东的方向为正，取A地为原点，则C地相对于A地的位置为（ ）
| A． | -2千米 | B． | -20千米 | C． | +2千米 | D． | +20千米 |