题目内容
3．
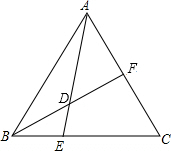如图，在△ABC中，E是BC上一点，EC=2BE，点F是AC的中点，若S△ABC=12，求S△ADF-S△BED的值．
分析 利用三角形面积公式，等高的三角形的面积比等于底边的比，则S△AEC=$\frac{2}{3}$S△ABC=8，S△BCF=$\frac{1}{2}$S△ABC=6，然后利用S△ADF-S△BED=S△AEC-S△BCF=2即可得到答案．
解答 解：∵EC=2BE，
∴S△AEC=$\frac{2}{3}$S△ABC=$\frac{2}{3}$×12=8，
∵点F是AC的中点，
∴S△BCF=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×12=6，
∴S△AEC-S△BCF=2，
即S△ADF+S四边形CEDF-（S△BDE+S四边形CEDF）=2，
∴S△ADF-S△BED=2．
点评 本题考查了三角形面积：三角形的面积等于底边长与高线乘积的一半，即S△=$\frac{1}{2}$×底×高；三角形的中线将三角形分成面积相等的两部分．
练习册系列答案
相关题目
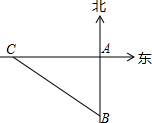如图，一艘轮船以30km/h的速度沿既定航线由西向东航行，途中接到台风警报，某台风中心正以20km/h的途度由南向北移动，距台风中心200km的圆形区域（包括边界）都属台风影响区．当这艘轮船接到台风警报时，它与台风中心的距离BC=500km，此时台风中心与轮船既定航线的最近距离BA=300km．
18．如果把分式$\frac{x+2y}{x+y}$中的x、y的值都变为原来的10倍，那么分式的值（ ）
| A． | 变成原来的10倍 | B． | 缩小为原来的10倍 | ||
| C． | 是原来的$\frac{2}{3}$ | D． | 不变 |
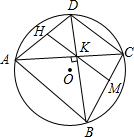如图．在⊙O的内接四边形ABCD中，AC⊥BD，垂足为K，M是BC的中点，直线MK交AD于点H．KH与AD有怎样的位置关系？为什么？
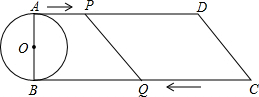如图，已知直角梯形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=24cm，BC=26cm，AB为⊙O的直径，动点P从点A开始沿AD边向点D以1cm/s的速度运动，动点Q从点C开始沿CB边向点B以3cm/s速度运动．P、Q分别从点A、C同时出发，当其中一点到达终点时，另一点也随之停止运动，设运动时间为t s，问：