题目内容
16.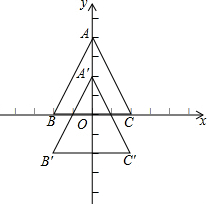 如图所示,已知△ABC三个顶点的坐标分别是A(0,4),B(-2,0),C(3,0),把△ABC沿y轴向下平移2个单位得△A′B′C′
如图所示,已知△ABC三个顶点的坐标分别是A(0,4),B(-2,0),C(3,0),把△ABC沿y轴向下平移2个单位得△A′B′C′(1)写出△A′B′C′各顶点的坐标;
(2)若A′B′交x轴于点D,A′C′交x轴于点E,求$\frac{{S}_{△A′DE}}{{S}_{△ABC}}$.
分析 (1)根据平移方法可得A、B、C三点坐标的纵坐标都减2,可得△A′B′C′各顶点的坐标;
(2)首先判定△A′DE∽△A′B′C′,根据相似三角形的面积比等于对应高之比的平方可得答案.
解答 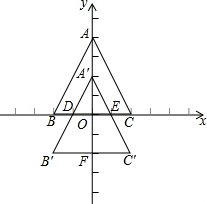 解:(1)∵A(0,4),B(-2,0),C(3,0),把△ABC沿y轴向下平移2个单位得△A′B′C′,
解:(1)∵A(0,4),B(-2,0),C(3,0),把△ABC沿y轴向下平移2个单位得△A′B′C′,
∴A′(0,2),B′(-2,-2),C′(3,-2);
(2)∵B′C′∥BC,
∴△A′DE∽△A′B′C′,
∵$\frac{A′O}{A′F}$=$\frac{2}{4}$=$\frac{1}{2}$,
∴$\frac{{S}_{△A′DE}}{{S}_{△ABC}}$=$\frac{1}{4}$.
点评 此题主要考查了作图--平移变换,关键是平移作图的一般步骤为:
①确定平移的方向和距离,先确定一组对应点;
②确定图形中的关键点;
③利用第一组对应点和平移的性质确定图中所有关键点的对应点;
④按原图形顺序依次连接对应点,所得到的图形即为平移后的图形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知a,b,c均是非零有理数,那么$\frac{|a|}{a}$+$\frac{b}{|b|}$+$\frac{|c|}{c}$的值应为( )
| A. | ±1 | B. | ±3 | C. | ±1或3 | D. | ±1或±3 |
6.如图,有12个方格,每个方格内有一个数,若相邻三个数的和都是20,则x的位置填的数为15
| -5 | a | b | c | d | e | f | x | g | h | j | 10 |
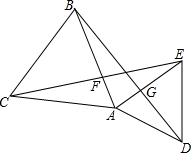 已知△ABC和△DAE是等边三角形,CE与AB交于点F,BD与AE交于点G,试问CE=BD吗?请说明你的结论.
已知△ABC和△DAE是等边三角形,CE与AB交于点F,BD与AE交于点G,试问CE=BD吗?请说明你的结论.