题目内容
某商场销售一批名牌衬衣,平均每天可售出20件,每件衬衣盈利40元.为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衣降价1元,商场平均每天可多售出2件.
(1)若商场平均每天盈利1200元,每件衬衣应降价多少元?
(2)若要使商场平均每天的盈利最多,请你为商场设计降价方案.
(1)20元;(2)每件衬衫降价15元时,商场平均每天赢利最多,最大利润为1250元.
【解析】
试题分析:(1)利用商场降价后每天盈利=每件的利润×卖出的件数=(40-降低的价格)×(20+增加的件数),把相关数值代入即可求解;
(2)利用商场降价后每天盈利=每件的利润×卖出的件数=(40-降低的价格)×(20+增加的件数),利用二次函数最值求法得出即可.
试题解析:(1)∵商场平均每天要盈利1200元,
∴(40-x)(20+2x)=1200,
整理得:2x2-60x+400=0,
解得:x1=20,x2=10,
因为要减少库存,在获利相同的情况下,降价越多,销售越快,故每件衬衫应降20元;
(2)设商场平均每天赢利w元,
则w=(20+2x)(40-x),
=-2x2+60x+800,
=-2(x-15)2+1250.
∴当x=15时,w取最大值,最大值为1250.
答:每件衬衫降价15元时,商场平均每天赢利最多,最大利润为1250元.
考点:1.二次函数的应用;2.一元二次方程的应用.

(本题8分)某人去水果批发市场采购苹果,他看中了A、B两家苹果。这两家苹果品质一样,零售价都为6元/千克,批发价各不相同。
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠。
B家的规定如下表:
数量范围(千克) | 0~500 | 500以上~1500 | 1500以上~2500 | 2500以上 |
价 格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
【表格说明:批发价格分段计算,如:某人批发苹果2100千克,则总费用=6×95%×500+6×85%×1000+6×75%×(2100-1500)】
(1)如果他批发600千克苹果,则他在A 家批发需要 元,在B家批发需要 元;
(2) 如果他批发x千克苹果(1500<x<2000),则他在A 家批发需要 元,在B家批发需要 元(用含x的代数式表示);
(3) 现在他要批发1800千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由。
 的图象与x轴只有一个公共点,求实数a的值.
的图象与x轴只有一个公共点,求实数a的值. =3,
=3, =4,且x>y,则2x-y的值为( )
=4,且x>y,则2x-y的值为( ) 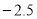 、
、 、2、
、2、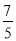 、
、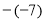 、0、-
、0、- 负有理数有 ( )
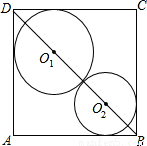
负有理数有 ( ) 与边长为5的等边△AOB的边OA,AB分别相交于C,D两点,且OC=3BD,则实数k的值为 .
与边长为5的等边△AOB的边OA,AB分别相交于C,D两点,且OC=3BD,则实数k的值为 .
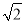 B.2.4 C.4-2
B.2.4 C.4-2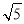 -1
-1