题目内容
(本题10分)抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点.
(1)求出m的值.
(2)求它与x轴的交点和抛物线顶点的坐标.
(3)x取值什么值时,抛物线在x轴上方?
(1)m=3;(2)与x轴的交点坐标:(-1,0)(3,0);顶点(1,4);(3)-1<x<3.
【解析】
试题分析:(1)把(0,3)代入函数解析式求出m的值;(2)令y=0,求出一元二次方程的两个解,就是函数与x轴的交点坐标,根据顶点坐标的求法求出顶点坐标;(3)根据二次函数图形的性质求出抛物线在x轴上方时的x的取值范围.
试题解析:(1)把(0,3)代入y=-x2+(m-1)x+m得,m=3. ∴ y=-x2+2x+3.
(2)当y=0时,0=-x2+2x+3.解得, ,
, ∴ 抛物线与x轴的交点是(-1,0)(3,0)
∴ 抛物线与x轴的交点是(-1,0)(3,0)
当 时,
时, ∴ 抛物线的顶点是(1,4)
∴ 抛物线的顶点是(1,4)
(3)∵a=-1<0 ∴抛物线的开口向下 又∵抛物线与x轴的交点是(-1,0)(3,0)
∴当 <
< <
< 时,抛物线在x轴上方.
时,抛物线在x轴上方.
考点:二次函数顶点坐标的求法及图象的性质.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目


 与代数式
与代数式 的值互为相反数,则x=___________.
的值互为相反数,则x=___________. ,下列去分母正确的是( )
,下列去分母正确的是( ) B.
B.
 D.
D.


 B.
B.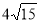 C.8 D.10
C.8 D.10 =0有两个相等的实数根,且满足
=0有两个相等的实数根,且满足 =
= ,试求
,试求 的值。
的值。