计算:①9x•${}^{2}$+(-3xy2)•(-x)2②③9982④(4a2+b2)⑤ 题目和参考答案——青夏教育精英家教网—

题目内容

16．计算：
①9x•${（\frac{2}{3}xy）}^{2}$+（-3xy²）•（-x）²
②（x-y）（3x+2y）
③998²（利用乘法公式计算）
④（2a-b）（4a²+b²）（2a+b）
⑤（m-n+3）（m+n-3）

分析 ①原式利用幂的乘方与积的乘方运算法则计算，合并即可得到结果；
②原式利用多项式乘以多项式法则计算即可得到结果；
③原式变形后，利用完全平方公式化简即可得到结果；
④原式利用平方差公式计算即可得到结果；
⑤原式利用平方差公式及完全平方公式化简即可得到结果．

解答解：①原式=4x³y²-3x³y²=x³y²；
②原式=3x²+2xy-3xy-2y²=3x²-xy-2y²；
③原式=（1000-2）²=1000000-4000+4=996004；
④原式=（4a²-b²）（4a²+b²）=16a⁴-b⁴；
⑤原式=m²-（n-3）²=m²-n²+6n-9．

点评此题考查了整式的混合运算，平方差公式，以及完全平方公式，熟练掌握公式及运算法则是解本题的关键．

练习册系列答案

相关题目

6．

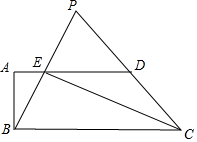已知：如图，在梯形ABCD中，AD∥BC，∠ABC=90°，AB=4，AD=8，sin∠BCD=$\frac{4}{5}$，CE平分∠BCD，交边AD于点E，联结BE并延长，交CD的延长线于点P．
（1）求梯形ABCD的周长；
（2）求PE的长．

7．阅读下列材料，然后解答问题：
在进行二次根式的化简与运算时，我们有时会碰上如：$\frac{3}{\sqrt{5}}$，$\sqrt{\frac{2}{3}}$，$\frac{2}{\sqrt{3}+1}$一样的式子．其实我们还可以将其进一步化简：
$\frac{3}{\sqrt{5}}$=$\frac{3×\sqrt{5}}{\sqrt{5}×\sqrt{5}}$=$\frac{3\sqrt{5}}{5}$：（一） $\sqrt{\frac{2}{3}}$=$\frac{\sqrt{2×3}}{\sqrt{3×3}}$=$\frac{\sqrt{6}}{3}$：（二）
$\frac{2}{\sqrt{3}+1}$=$\frac{2（\sqrt{3}-1）}{（\sqrt{3}+1）（\sqrt{3}-1）}$=$\frac{2（\sqrt{3}-1）}{（\sqrt{3}）^{2}-1}$=$\sqrt{3}-1$：（三）
以上这种化简的步骤叫做分母有理化．
$\frac{2}{\sqrt{3}+1}$还可以用以下方法化简：
$\frac{2}{\sqrt{3}+1}$=$\frac{3-1}{\sqrt{3}+1}$=$\frac{（\sqrt{3}）^{2}-1}{\sqrt{3}+1}$=$\frac{（\sqrt{3}+1）（\sqrt{3}-1）}{\sqrt{3}+1}$=$\sqrt{3}-1$．（四）
请解答下列问题：
（1）请用不同的方法化简$\frac{2}{\sqrt{5}+\sqrt{3}}$．
①参照（三）式得$\frac{2}{\sqrt{5}+\sqrt{3}}$=$\sqrt{5}$-3；
②参照（四）式得$\frac{2}{\sqrt{5}+\sqrt{3}}$=$\frac{（\sqrt{5}）^{2}-（\sqrt{3}）^{2}}{\sqrt{5}+\sqrt{3}}$=$\frac{（\sqrt{5}+\sqrt{3}）（\sqrt{5}-\sqrt{3}）}{\sqrt{5}+\sqrt{3}}$=$\sqrt{5}$-$\sqrt{3}$；
（2）化简：$\frac{2}{\sqrt{3}+1}$+$\frac{2}{\sqrt{5}+\sqrt{3}}$+$\frac{2}{\sqrt{7}+\sqrt{5}}$；（保留过程）
（3）猜想：$\frac{1}{\sqrt{3}+1}$+$\frac{1}{\sqrt{5}+\sqrt{3}}$+$\frac{1}{\sqrt{7}+\sqrt{5}}$+…+$\frac{1}{\sqrt{2n+1}+\sqrt{2n-1}}$的值．（直接写出结论）

4．

已知关于x的不等式x-a≥-2的解集在数轴上表示如图，则a的值为1．

11．某次国学知识竞赛初赛共20道题，（满分100分），评分办法是：答对1道题得5分，答错或不答倒扣2分，选手至少答对多少题才能得到70分以上（含70分）？

1．解方程组
（1）$\left\{\begin{array}{l}{4（x-y-1）=3（1-y）-2}\\{\frac{x}{2}+\frac{y}{3}=2}\end{array}\right.$
（2）$\left\{\begin{array}{l}{\frac{3x-5y}{3}-2=0}\\{\frac{1}{2}x+2y+\frac{15}{2}=0}\end{array}\right.$．

8．化简：2$\overrightarrow{a}$-3（$\frac{1}{3}$$\overrightarrow{a}$-$\overrightarrow{b}$）=$\overrightarrow{a}$+3$\overrightarrow{b}$．

5．（1）计算：|1-$\sqrt{3}$|-3tan30°+（π-2017）⁰-（-$\frac{1}{3}$）^-1
（2）解不等式组$\left\{\begin{array}{l}{2x＜5①}\\{3（x+2）≥x+4②}\end{array}\right.$并在数轴上表示它的解集．

6．不等式组$\left\{\begin{array}{l}{3x+1＜2（x+1）}\\{-x＜5x+12}\end{array}\right.$的整数解为-1，0．

试题分类