题目内容
1. 如图,动点A从原点出发向数轴正方向运动,同时,动点B也从原点出发向数轴负方向运动.已知点A比点B每秒多运动2个单位长度,4秒后两点相距24个单位长度.
如图,动点A从原点出发向数轴正方向运动,同时,动点B也从原点出发向数轴负方向运动.已知点A比点B每秒多运动2个单位长度,4秒后两点相距24个单位长度.(1)求出两个动点运动的速度,并在数轴上标出A、B两点从原点出发4秒时的位置;
(2)若A、B两点从(1)中标出的位置同时按原速度向数轴正方向运动,几秒时,点A到原点的距离是点B到原点距离的4倍?
分析 (1)设动点A的速度是x单位长度/分,那么动点B的速度是3x单位长度/分,然后根据3分后,两点相距24个单位长度即可列出方程解决问题;
(2)根据题意列出方程,即可解答.
解答 解:(1)设动点B的速度是x单位长度/分,则点A的速度是(x+2)单位长度/分,
根据题意得4(x+x+2)=24
解得:x=2,
则x+2=4.
答:动点A的速度是4单位长度/分,动点B的速度是2单位长度/分;
如图:
(2)设y分时,点A到原点的距离是点B到原点距离的4倍,
根据题意得:16+4y=4|2y-8|
解得:y=12或0.5,
答:12秒或1.5时,点A到原点的距离是点B到原点距离的4倍.
点评 此题主要考查了一元一方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19. 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )
 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
20.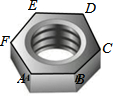 如图,螺母的一个面的外沿可以看作是正六边形,这个正六边形ABCDEF的半径是$2\sqrt{3}$cm,则这个正六边形的周长是( )
如图,螺母的一个面的外沿可以看作是正六边形,这个正六边形ABCDEF的半径是$2\sqrt{3}$cm,则这个正六边形的周长是( )
 如图,螺母的一个面的外沿可以看作是正六边形,这个正六边形ABCDEF的半径是$2\sqrt{3}$cm,则这个正六边形的周长是( )
如图,螺母的一个面的外沿可以看作是正六边形,这个正六边形ABCDEF的半径是$2\sqrt{3}$cm,则这个正六边形的周长是( )| A. | $6\sqrt{3}$cm | B. | 12cm | C. | $12\sqrt{3}$cm | D. | 36 cm |
 如图,已知AD∥BC,∠1=∠2,判断∠BEF与∠DFE的大小关系并说明理由.
如图,已知AD∥BC,∠1=∠2,判断∠BEF与∠DFE的大小关系并说明理由. 已知数轴上数a、b、c对应点的位置如图所示,化简|c-b|+|c-a|-|b-a|.
已知数轴上数a、b、c对应点的位置如图所示,化简|c-b|+|c-a|-|b-a|. 如图,已知直线a∥b,且∠1=60°,则∠2=120°.
如图,已知直线a∥b,且∠1=60°,则∠2=120°.