题目内容
12. 一种产品的进价为40元,某公司在销售这种产品时,每年总开支为100万元(不含进价).经过若干年销售得知,年销售量y(万件)是销售单价x(元)的一次函数,并得到如下部分数据:
一种产品的进价为40元,某公司在销售这种产品时,每年总开支为100万元(不含进价).经过若干年销售得知,年销售量y(万件)是销售单价x(元)的一次函数,并得到如下部分数据:| 销售单价x(元) | 50 | 60 | 70 | 80 |
| 年销售量y(万件) | 5.5 | 5 | 4.5 | 4 |
(2)写出该公司销售这种产品的年利润w(万元)关于销售单价x(元)的函数关系式;当销售单价x为何值时,年利润最大?
(3)试通过(2)中的函数关系式及其大致图象帮助该公司确定产品的销售单价范围,使年利润不低于60万元.
分析 (1)根据表中的已知点的坐标利用待定系数法确定直线的解析式即可;
(2)根据总利润=单件利润×销量列出函数关系式配方后即可确定最值;
(3)令利润等于60求得相应的自变量的值即可确定销售单价的范围.
解答 解:(1)设y=kx+b,把(60,5),(80,4)代入得:$\left\{\begin{array}{l}{60k+b=5}\\{80k+b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{20}}\\{b=8}\end{array}\right.$,
故答案为:y=-$\frac{1}{20}$x+8;
(2)该公司年利润w=(-$\frac{1}{20}$x+8)(x-40)-100=-$\frac{1}{20}$(x-100)2+80,
当x=100时,该公司年利润最大值为80万元;
(3)由题意得:-$\frac{1}{20}$(x-100)2+80=60,
解得:x1=80,x2=120,
故该公司确定销售单价x的范围是:80≤x≤120.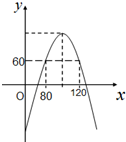
根据函数图象可得:当80≤x≤120时,
该公司产品的利润不低于60万元.
点评 本题考查了二次函数的应用,解题时把实际问题转化为二次函数,再对二次函数进行实际应用.此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
相关题目
2. 已知OA,OB是⊙O的半径,点C在⊙O上,∠OBA=50°,则∠C的度数为( )
已知OA,OB是⊙O的半径,点C在⊙O上,∠OBA=50°,则∠C的度数为( )
 已知OA,OB是⊙O的半径,点C在⊙O上,∠OBA=50°,则∠C的度数为( )
已知OA,OB是⊙O的半径,点C在⊙O上,∠OBA=50°,则∠C的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 80° |
3.小明有两根3cm、7cm的木棒,他想以这两根木棒为边做一个三角形,还需再选用的木棒长为( )
| A. | 3cm | B. | 4cm | C. | 9cm | D. | 10cm |
17.近年来,国家大力提倡大学生创业,2015年小王就要毕业了,因为他学的是市场营销专业,所以毕业后想开一个商店,经过市场调研发现,若投资一个面积为x(单位:m2)的商铺,所需购买费用(单位:万元)与x+2成正比例,装修费用(单位:万元)与x2成正比例,并在调查过程中得到了表格中的数据:
(1)如果小王用从银行贷款30万元、父亲资助20万元、自己大学期间勤工俭学的收入1.6万元,共51.6万元投资一个商铺,请计算小王投资的这个商铺的面积为多少平方米;(总费用=购买费用+装修费用)
(2)购买商铺后,小王准备经营童鞋专卖店,已知专卖店代理的某品牌童鞋的进价为每双40元,该品牌童鞋日销售量y(双)与销售单价x(元/双)之间的关系式为:
y=$\left\{\begin{array}{l}{-2x+140(40≤x≤58)}\\{-x+82(58<x≤71)}\end{array}\right.$
①求他的销售利润w(元)与销售单价x(元/双)之间的函数关系式.
②小王每月需向银行还贷2075元,另童鞋店每月需缴纳水电费、营业税等固定费用3000元,通过计算判断,小王每月(按30天计算)能否有盈余?如果有,最多盈余多少元?(盈余=销售利润-固定费用-银行贷款)
| 商铺的面积(m2) | 购买费用(万元) | 装修费用(万元) |
| 1 | 1.8 | 0.3 |
(2)购买商铺后,小王准备经营童鞋专卖店,已知专卖店代理的某品牌童鞋的进价为每双40元,该品牌童鞋日销售量y(双)与销售单价x(元/双)之间的关系式为:
y=$\left\{\begin{array}{l}{-2x+140(40≤x≤58)}\\{-x+82(58<x≤71)}\end{array}\right.$
①求他的销售利润w(元)与销售单价x(元/双)之间的函数关系式.
②小王每月需向银行还贷2075元,另童鞋店每月需缴纳水电费、营业税等固定费用3000元,通过计算判断,小王每月(按30天计算)能否有盈余?如果有,最多盈余多少元?(盈余=销售利润-固定费用-银行贷款)
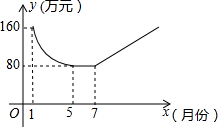 保护生态环境,建设绿色社会已经从理念变为人们的行动,某化工厂2011年1月的利润为160万元,设2011年1月为第1个月,第x个月的利润为y万元,由于排污超标,该厂决定从2011年1月底起适当限产,并投入资金进行治污改造,整个工程经过治污改造、调试、全面投产是三个时期,经测算:从1月到5月为治污改造期,y是x的二次函数,且其图象的顶点为(5,80),到5月底治污改造工程顺利完成,进接的6月、7月为调试期,月利润和5月份持平,调试期过后,设备全面投产,该厂每月利润比前一个月增加15万元,如图所示.
保护生态环境,建设绿色社会已经从理念变为人们的行动,某化工厂2011年1月的利润为160万元,设2011年1月为第1个月,第x个月的利润为y万元,由于排污超标,该厂决定从2011年1月底起适当限产,并投入资金进行治污改造,整个工程经过治污改造、调试、全面投产是三个时期,经测算:从1月到5月为治污改造期,y是x的二次函数,且其图象的顶点为(5,80),到5月底治污改造工程顺利完成,进接的6月、7月为调试期,月利润和5月份持平,调试期过后,设备全面投产,该厂每月利润比前一个月增加15万元,如图所示.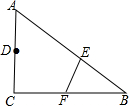 如图,在△ABC中,∠C=90°,AC=6,BC=9,将△ABC沿EF翻折点B恰好落在CA的中点D处,则折痕EF的长为$\sqrt{10}$.
如图,在△ABC中,∠C=90°,AC=6,BC=9,将△ABC沿EF翻折点B恰好落在CA的中点D处,则折痕EF的长为$\sqrt{10}$.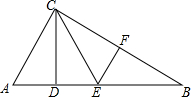 如图所示,在△ABC中,∠ACB=90°,△BEF与△CEF成轴对称,△CEF沿CE翻折与△CED重合,且△ACD≌△EBF.
如图所示,在△ABC中,∠ACB=90°,△BEF与△CEF成轴对称,△CEF沿CE翻折与△CED重合,且△ACD≌△EBF. 如图,一次函数y=-x+4的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B两点.
如图,一次函数y=-x+4的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B两点.