题目内容
1. 如图,一次函数y=-x+4的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B两点.
如图,一次函数y=-x+4的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B两点.(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
分析 (1)把点A(1,a)代入一次函数y=-x+4,即可得出a,再把点A坐标代入反比例函数y=$\frac{k}{x}$,即可得出k,两个函数解析式联立求得点B坐标;
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,此时PA+PB的值最小,求出直线AD的解析式,令y=0,即可得出点P坐标.
解答 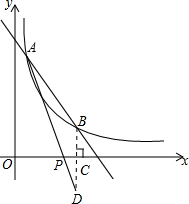 解:(1)把点A(1,a)代入一次函数y=-x+4,
解:(1)把点A(1,a)代入一次函数y=-x+4,
得a=-1+4,
解得a=3,
∴A(1,3),
点A(1,3)代入反比例函数y=$\frac{k}{x}$,
得k=3,
∴反比例函数的表达式y=$\frac{3}{x}$,
两个函数解析式联立列方程组得$\left\{\begin{array}{l}{y=-x+4}\\{y=\frac{3}{x}}\end{array}\right.$,
解得x1=1,x2=3,
∴点B坐标(3,1);
(2)过点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,此时PA+PB的值最小,
∴D(3,-1),
设直线AD的解析式为y=mx+n,
把A,D两点代入得,$\left\{\begin{array}{l}{m+n=3}\\{3m+n=-1}\end{array}\right.$,
解得m=-2,n=5,
∴直线AD的解析式为y=-2x+5,
令y=0,得x=$\frac{5}{2}$,
∴点P坐标($\frac{5}{2}$,0),
S△PAB=S△ABD-S△PBD=$\frac{1}{2}$×2×2-$\frac{1}{2}$×2×$\frac{1}{2}$=2-$\frac{1}{2}$=$\frac{3}{2}$.
点评 本题考查了一次函数和反比例函数相交的有关问题;通常先求得反比例函数解析式;较复杂三角形的面积可被x轴或y轴分割为2个三角形的面积和.

| A. | x2-9+6x=(x+3)(x-3)+6x | B. | x2-8x+16=(x-4)2 | ||
| C. | (x-1)2=x2-2x+1 | D. | x2+1=x(x+$\frac{1}{x}$) |
 一种产品的进价为40元,某公司在销售这种产品时,每年总开支为100万元(不含进价).经过若干年销售得知,年销售量y(万件)是销售单价x(元)的一次函数,并得到如下部分数据:
一种产品的进价为40元,某公司在销售这种产品时,每年总开支为100万元(不含进价).经过若干年销售得知,年销售量y(万件)是销售单价x(元)的一次函数,并得到如下部分数据:| 销售单价x(元) | 50 | 60 | 70 | 80 |
| 年销售量y(万件) | 5.5 | 5 | 4.5 | 4 |
(2)写出该公司销售这种产品的年利润w(万元)关于销售单价x(元)的函数关系式;当销售单价x为何值时,年利润最大?
(3)试通过(2)中的函数关系式及其大致图象帮助该公司确定产品的销售单价范围,使年利润不低于60万元.
 如图,正方形ABCD和正△AEF都内接于⊙O,EF与BC、CD分别相交于点G、H,则$\frac{EF}{GH}$的值是( )
如图,正方形ABCD和正△AEF都内接于⊙O,EF与BC、CD分别相交于点G、H,则$\frac{EF}{GH}$的值是( )| A. | $\frac{\sqrt{6}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
| A. | x-1 | B. | x+1 | C. | x2-1 | D. | (x-1)2 |
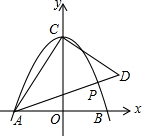 如图,抛物线y=ax2+4与x轴交于A、B两点(A在B的左边),与y轴交于点C,AB=4.
如图,抛物线y=ax2+4与x轴交于A、B两点(A在B的左边),与y轴交于点C,AB=4.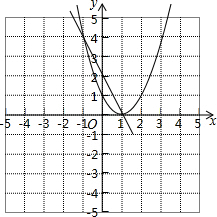 设函数y=(x-1)[(k-1)x+(k-3)](k是常数).
设函数y=(x-1)[(k-1)x+(k-3)](k是常数). 已知抛物线y=-x2+bx+c与x轴交于点A(m-2,0)和B(2m+1,0)(点A在点B的左侧),与y轴相交于点C,顶点为P,对称轴为l:x=1.
已知抛物线y=-x2+bx+c与x轴交于点A(m-2,0)和B(2m+1,0)(点A在点B的左侧),与y轴相交于点C,顶点为P,对称轴为l:x=1.