题目内容
14.计算:(12x3-8x2+16x)÷(-4x)的结果是( )| A. | -3x2+2x-4 | B. | -3x2-2x+4 | C. | -3x2+2x+4 | D. | 3x2-2x+4 |
分析 多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把所得的商相加;12x3÷(-4x)=-3x2,-8x2÷(-4x)=2x,16x÷(4x)=-4.
解答 解:(12x3-8x2+16x)÷(-4x)=-3x2+2x-4;
故选A.
点评 本题考查了整式的除法,此题的关键是单项式除以单项式、多项式除以单项式,要注意符号,熟练掌握法则进行计算,

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.下列说法正确的是( )
| A. | x2-x=0是二项方程 | B. | $\frac{x-1}{2}-\frac{x}{3}=4$是分式方程 | ||
| C. | $\sqrt{2}{x^2}-2x=\sqrt{3}$是无理方程 | D. | 2x2-y=4是二元二次方程 |
6.开学初,学校要补充部分体育器材,从超市购买了一些排球和篮球.其中购买排球的总价为1000元,购买篮球的总价为1600元,且购买篮球的数量是购买排球数量的2倍.已知购买一个排球比一个篮球贵20元.
(1)求购买排球和篮球的单价各是多少元;
(2)为响应“足球进校园”的号召,学校计划再购买50个足球.恰逢另一超市对A、B两种品牌的足球进行降价促销,销售方案如表所示.如果学校此次购买A、B两种品牌足球的总费用不超过5000元.那么最多可购买多少个品牌足球?
(1)求购买排球和篮球的单价各是多少元;
(2)为响应“足球进校园”的号召,学校计划再购买50个足球.恰逢另一超市对A、B两种品牌的足球进行降价促销,销售方案如表所示.如果学校此次购买A、B两种品牌足球的总费用不超过5000元.那么最多可购买多少个品牌足球?
| 种类 | 标价 | 优惠方案 |
| A品牌足球 | 150元/个 | 八折 |
| B品牌足球 | 100元/个 | 九折 |
3.用配方法解方程3x2+8x-3=0,下列变形正确的是( )
| A. | (x+$\frac{16}{3}$)2=1+($\frac{16}{3}$)2 | B. | (x+$\frac{4}{3}$)2=1+($\frac{4}{3}$)2 | C. | (x-$\frac{8}{3}$)2=1+($\frac{1}{3}$)2 | D. | (x-$\frac{4}{3}$)2=1-($\frac{4}{3}$)2 |
14.下列计算正确的是( )
| A. | 2x2-4x2=-2 | B. | 3x+x=3x2 | C. | 3x•x=3x2 | D. | 4x6÷2x2=2x3 |
 如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若乘车的学生有150人,则据此估计步行的有400人.
如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若乘车的学生有150人,则据此估计步行的有400人.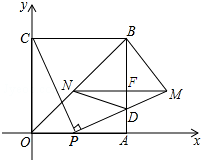 如图,四边形OABC是边长为4的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥AO,交BO于点N,连结ND、BM,设OP=t.
如图,四边形OABC是边长为4的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥AO,交BO于点N,连结ND、BM,设OP=t.