题目内容
20.请将下列实数填入相应的括号内:0,2003,3.14$\stackrel{.}{4}$,-$\frac{3}{4}$,-$\frac{π}{3}$,(-4)3,-$\sqrt{2}$,$\root{3}{-27}$,$\sqrt{0.9}$,5.12345678910111213…(小数部分由连续的正整数组成)有理数集合:{0,2003,3.14$\stackrel{.}{4}$,-$\frac{3}{4}$,$\root{3}{-27}$,(-4)3…}
无理数集合:{-$\frac{π}{3}$,-$\sqrt{2}$,$\sqrt{0.9}$,5.12345678910111213…(小数部分由连续的正整数组成)…}.
分析 根据有限小数或无限循环小数是有理数,无理数是无限不循环小数,可得答案.
解答 解:有理数集合:{ 0,2003,3.14$\stackrel{.}{4}$,-$\frac{3}{4}$,$\root{3}{-27}$,(-4)3…}
无理数集合:{-$\frac{π}{3}$,-$\sqrt{2}$,$\sqrt{0.9}$,5.12345678910111213…(小数部分由连续的正整数组成)…},
故答案为:0,2003,3.14$\stackrel{.}{4}$,-$\frac{3}{4}$,$\root{3}{-27}$,(-4)3;-$\frac{π}{3}$,-$\sqrt{2}$,$\sqrt{0.9}$,5.12345678910111213…(小数部分由连续的正整数组成).
点评 本题考查了实数,有理数和无理数统称实数;有限小数或无限循环小数是有理数,无理数是无限不循环小数.

练习册系列答案
相关题目
11.如图1,四边形ABCD、AEFG都是正方形,连接DE、BG.
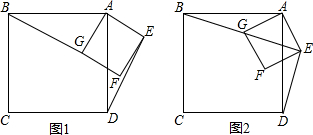
(1)求证:DE=BG;
(2)在图(2)中,连接GE,若点B、G、E在同一直线上时,AB=$\sqrt{3}$,DE=1,求AE的长.

(1)求证:DE=BG;
(2)在图(2)中,连接GE,若点B、G、E在同一直线上时,AB=$\sqrt{3}$,DE=1,求AE的长.
15.关于x的方程$\frac{2x+a}{x-1}$=1的解是负数,则a的取值范围是( )
| A. | a>-1 | B. | a>-1或a≠-2 | C. | a<-1 | D. | a<-1且a≠0 |
10.-42的意义是( )
| A. | 2个-4相乘 | B. | 2个-4相加 | C. | 42的相反数 | D. | -4乘以2 |
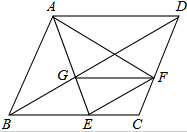 已知,如图,在菱形ABCD中,点E、F分别在边BC、CD,∠BAF=∠DAE,AE与BD交于点G.
已知,如图,在菱形ABCD中,点E、F分别在边BC、CD,∠BAF=∠DAE,AE与BD交于点G.