题目内容
12.从点A(-1,8),B(1,0),C(2,1)中任取一个点,该点恰好在抛物线y=x2-4x+3上的概率是多少?分析 由从点A(-1,8),B(1,0),C(2,1)中任取一个点,该点恰好在抛物线y=x2-4x+3上的有:A(-1,8),B(1,0),直接利用概率公式求解即可求得答案.
解答 解:∵从点A(-1,8),B(1,0),C(2,1)中任取一个点,该点恰好在抛物线y=x2-4x+3上的有:A(-1,8),B(1,0),
∴该点恰好在抛物线y=x2-4x+3上的概率是:$\frac{2}{3}$.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
7.抛物线y=(x-2)2-3的顶点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1.已知一元二次方程:①x2-2x-3=0,②x2+2x+3=0.下列说法正确的是( )
| A. | ①②都有实数解 | B. | ①无实数解,②有实数解 | ||
| C. | ①有实数解,②无实数解 | D. | ①②都无实数解 |
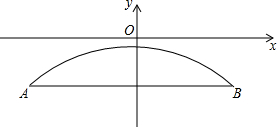 有一个抛物线形的拱形桥,若抛物线的解析式为y=-$\frac{1}{75}$x2-1.
有一个抛物线形的拱形桥,若抛物线的解析式为y=-$\frac{1}{75}$x2-1. 如图,在正方形ABCD时,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.则下列结论:①△ABE≌△DCF;②DP2=PH•PB;③$\frac{FP}{PH}=\frac{17}{30}$;④$\frac{{{S_{△BPD}}}}{{{S_{正方形ABCD}}}}=\frac{{\sqrt{3}-1}}{4}$.其中正确的是①②④(写出所有正确结论的序号).
如图,在正方形ABCD时,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.则下列结论:①△ABE≌△DCF;②DP2=PH•PB;③$\frac{FP}{PH}=\frac{17}{30}$;④$\frac{{{S_{△BPD}}}}{{{S_{正方形ABCD}}}}=\frac{{\sqrt{3}-1}}{4}$.其中正确的是①②④(写出所有正确结论的序号).