题目内容
1.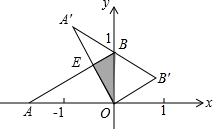 如图,点A的坐标为(-$\sqrt{3}$,0),点B的坐标为(0,1),将△AOB绕原点O顺时针旋转60°到△A'OB',A'B'恰好过点B,则B'的坐标为($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),重叠部分△BOE的面积为$\frac{\sqrt{3}}{8}$.
如图,点A的坐标为(-$\sqrt{3}$,0),点B的坐标为(0,1),将△AOB绕原点O顺时针旋转60°到△A'OB',A'B'恰好过点B,则B'的坐标为($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),重叠部分△BOE的面积为$\frac{\sqrt{3}}{8}$.
分析 过点B′作B′F⊥x轴于点F,根据旋转性质可得OB=OB′=1、∠AOA′=∠BOB′=60°即∠BOE=∠B′OF=30°,在Rt△B′OF中,根据三角函数求得OF、B′F可得点B′坐标;根据题意可得∠ABO=60°,继而可得∠OEB=90°,再求得OE、BE,从而得出△BOE的面积.
解答 解:过点B′作B′F⊥x轴于点F,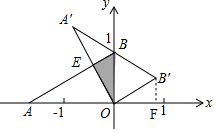
根据旋转性质可得:OB=OB′=1,∠AOA′=∠BOB′=60°,
∴∠BOE=∠B′OF=30°,
在Rt△B′OF中,OF=OB′cos∠B′OF=1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$,
B′F=OB′sin∠B′OF=1×$\frac{1}{2}$=$\frac{1}{2}$,
∴点B′的坐标为($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),
在Rt△AOB中,∵OB=1,AO=$\sqrt{3}$,
∴tan∠ABO=$\frac{AO}{BO}$=$\sqrt{3}$,
∴∠ABO=60°,
∴∠OEB=90°,
在Rt△BOE中,OE=OBsin∠ABO=$\frac{\sqrt{3}}{2}$,BE=OBcos∠ABO=$\frac{1}{2}$,
∴S△BOE=$\frac{1}{2}$BE•OE=$\frac{\sqrt{3}}{8}$,
故答案为:($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),$\frac{\sqrt{3}}{8}$.
点评 本题主要考查旋转的性质和解直角三角形,熟练掌握旋转的性质得出所需角的度数和线段的长度是解题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
11.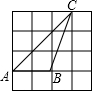 如图,小正方形的边长均为1,有格点△ABC,则sinC=( )
如图,小正方形的边长均为1,有格点△ABC,则sinC=( )
 如图,小正方形的边长均为1,有格点△ABC,则sinC=( )
如图,小正方形的边长均为1,有格点△ABC,则sinC=( )| A. | $\frac{2}{3}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
13.相同时刻太阳光下,若高为1.5m的测杆的影长为3m,则影长为30m的旗杆的高是( )
| A. | 15m | B. | 16m | C. | 18m | D. | 20m |
 在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:有一个水池,截面是一个边长为12尺的正方形,在水池正中央有一根新生的芦苇,它高出水面2尺,如下图所示,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.那么水深多少?芦苇长为多少?
在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:有一个水池,截面是一个边长为12尺的正方形,在水池正中央有一根新生的芦苇,它高出水面2尺,如下图所示,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.那么水深多少?芦苇长为多少?


