题目内容
(1)解方程组
;
(2)解不等式组:
;
(3)已知方程组
的解是负数.①求a的取值范围;②化简:|a+3|-|5a-3|.
|
(2)解不等式组:
|
(3)已知方程组
|
考点:解二元一次方程组,二元一次方程组的解,解一元一次不等式组
专题:计算题
分析:(1)方程组利用加减消元法求出解即可;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可;
(3)①将a看做已知数表示出x与y,根据方程组的解为负数求出a的范围;
②由a的范围判断出绝对值里边式子的正负,利用绝对值的代数意义化简计算,即可得到结果.
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可;
(3)①将a看做已知数表示出x与y,根据方程组的解为负数求出a的范围;
②由a的范围判断出绝对值里边式子的正负,利用绝对值的代数意义化简计算,即可得到结果.
解答:解:(1)
,
①-②得:4y=4,即y=1,
将y=1代入②得:x=1,
则方程组的解为
;
(2)不等式组
,
由①得:x>-3;
由②得:x≤
,
则不等式组的解集为-3<x≤
;
(3)①
,
①+②得:3x=-a-3,即x=
,
将x=
代入得:y=
+2a,
根据题意得:
,
解得:-3<a<
;
②∵-3<a<
,
∴a+3>0,5a-3<0,
则原式=a+3-3+5a=6a.
|
①-②得:4y=4,即y=1,
将y=1代入②得:x=1,
则方程组的解为
|
(2)不等式组
|
由①得:x>-3;
由②得:x≤
| 8 |
| 3 |
则不等式组的解集为-3<x≤
| 8 |
| 3 |
(3)①
|
①+②得:3x=-a-3,即x=
| -a-3 |
| 3 |
将x=
| -a-3 |
| 3 |
| -a-3 |
| 3 |
根据题意得:
|
解得:-3<a<
| 3 |
| 5 |
②∵-3<a<
| 3 |
| 5 |
∴a+3>0,5a-3<0,
则原式=a+3-3+5a=6a.
点评:此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
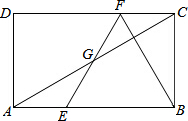 如图,在矩形ABCD中,E、F分别是AB、CD上的点,AE=CF,连接EF、BF,EF交对角线AC于点G,若BE=BF,∠DFE=2∠BAC,BC=
如图,在矩形ABCD中,E、F分别是AB、CD上的点,AE=CF,连接EF、BF,EF交对角线AC于点G,若BE=BF,∠DFE=2∠BAC,BC=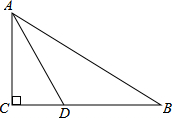 如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC与BC相交于点D,若AD=4,CD=2,则AB的长是
如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC与BC相交于点D,若AD=4,CD=2,则AB的长是