题目内容
4．
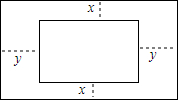姥姥有一张长2米、宽1米的十字绣，她在十字绣的四周加上了花边做成了挂毯，上下花边宽度为x米，左右花边宽度为y米，若十字绣与挂毯是相似的长方形．（1）求y与x的函数关系式；
（2）若姥姥准备挂在客厅墙上，墙长为4米，高为2.8米，挂毯的面积为S，求S与x的函数关系式．
分析 （1）求得挂毯的长与宽，利用相似得出y与x的函数关系式即可；
（2）利用长方形的面积，代入求得S与x的函数关系式即可．
解答 解：（1）挂毯的长为（2+2y）米，宽为（2+2x）米，由题意得
$\frac{2+2y}{2}$=$\frac{1+2x}{1}$
则y=2x；
（2）挂毯的面积为S=（2+2y）（1+2x）
=（2+4x）（1+2x）
=8x2+6x+2．
点评 此题考查由实际问题列一次函数与二次函数解析式，掌握相似的性质和长方形的面积计算方法是解决问题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
9．下列计算正确的是（ ）
| A． | （$\frac{2{a}^{-3}b}{-{c}^{3}}$）2=$\frac{4{a}^{9}b}{{c}^{5}}$ | B． | （$\frac{2x-y}{-5{a}^{2}}$）2=$\frac{4{x}^{2}-{y}^{2}}{25{a}^{4}}$ | ||
| C． | （3xny-n）-m=$\frac{{y}^{mn}}{{3}^{m}x^{mn}}$ | D． | （-$\frac{{b}^{2}}{a}$）2n=-$\frac{{b}^{2+2n}}{{a}^{n}}$ |
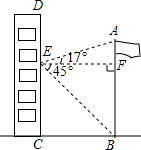如图，在某次数学活动课中，小明为了测量校园内旗杆AB的高度，站在教学楼CD上的E处测得旗杆底端B的仰角∠BEF的度数为45°，测得旗杆顶端A的仰角∠AEF的度数为17°，旗杆底部B处与教学楼底部C处的水平距离BC为9m，求旗杆的高度（结果精确到0.1m）．
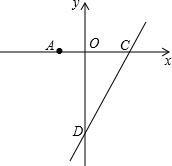如图，点A的坐标为（-1，0），点B在直线y=2x-4上运动．