题目内容
8.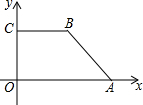 如图所示的平面直角坐标系中,在直角梯形OABC中,CB∥OA,CB=8,OC=6,∠OAB=45°.
如图所示的平面直角坐标系中,在直角梯形OABC中,CB∥OA,CB=8,OC=6,∠OAB=45°.(1)求点A、B、C的坐标;
(2)求梯形OABC的面积.
分析 (1)因为A,C分别在横纵轴正半轴上,OA=8,OC=6,所以可以直接得出A,C点坐标,根据BC与OA关系和BC的长就可得出B的坐标.
(2)根据梯形面积公式求解即可.
解答 解:(1)∵OC=6,
∴C坐标为(0,6),
如图,过B作BD⊥OA于D,
∴四边形ODBC是矩形,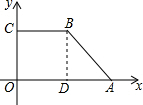
∴OD=BC=8,BD=OC=6,
∵∠OAB=45°,
∴AD=BD=6,
∴OA=14,
∴B(8,6),A(14,0);
(2)根由梯形面积公式可得:
S梯形OABC=$\frac{1}{2}$(BC+OA)×OC=11×6=66.
点评 本题考查了坐标与图形的性质,做题时注意坐标的确定以及所围图形的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.以下生活现象中,属于旋转变换得是( )
| A. | 钟表的指针和钟摆的运动 | B. | 站在电梯上的人的运动 | ||
| C. | 坐在火车上睡觉 | D. | 地下水位线逐年下降 |
18.猜猜“它”是谁:“它”的倒数等于16与-4的商,“它”是( )
| A. | -4 | B. | $-\frac{1}{4}$ | C. | 4 | D. | $-\frac{1}{4}$ |
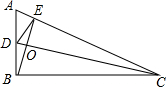 如图,D、E分别是△ABC的边AB、AC上的点,BE、CD相交于点O,且AD•AB=AE•AC,△OEC与△ODB相似吗?为什么?
如图,D、E分别是△ABC的边AB、AC上的点,BE、CD相交于点O,且AD•AB=AE•AC,△OEC与△ODB相似吗?为什么?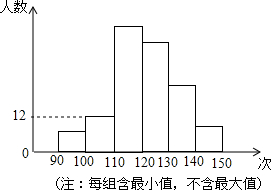 九年级学生进行了中考体育测试,某校抽取了部分学生的一分钟跳绳测试成绩,测试成绩整理后作出如图统计图,甲同学计算出前两组的频率和是0.12,乙同学计算出第一组的频率和为0.04,丙同学计算出从左至右第二、三、四组的频数比为4:17:15,结合统计图回答下列问题
九年级学生进行了中考体育测试,某校抽取了部分学生的一分钟跳绳测试成绩,测试成绩整理后作出如图统计图,甲同学计算出前两组的频率和是0.12,乙同学计算出第一组的频率和为0.04,丙同学计算出从左至右第二、三、四组的频数比为4:17:15,结合统计图回答下列问题