题目内容
11.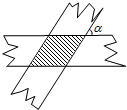 如图:两张宽度都为1cm的纸条交叉重叠在一起,两张纸条交叉的夹角为α(见图中的标注),则重叠(阴影)部分的面积表示为$\frac{1}{sinα}$.
如图:两张宽度都为1cm的纸条交叉重叠在一起,两张纸条交叉的夹角为α(见图中的标注),则重叠(阴影)部分的面积表示为$\frac{1}{sinα}$.
分析 首先过A作AE⊥BC,AF⊥CD于F,垂足为E,F,证明△ABE≌△ADF,从而证明四边形ABCD是菱形,再利用三角函数算出BC的长,最后根据菱形的面积公式算出重叠部分的面积即可.
解答 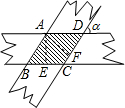 解:如图所示:过A作AE⊥BC,AF⊥CD于F,垂足为E,F,
解:如图所示:过A作AE⊥BC,AF⊥CD于F,垂足为E,F,
∴∠AEB=∠AFD=90°,
∵AD∥CB,AB∥CD,
∴四边形ABCD是平行四边形,
∵纸条宽度都为1cm,
∴AE=AF=1cm,
在△ABE和△ADF中,
$\left\{\begin{array}{l}{∠ABE=∠ADF=α}\\{∠AEB=∠AFD=90°}\\{AE=AF}\end{array}\right.$,
∴△ABE≌△ADF(AAS),
∴AB=AD,
∴四边形ABCD是菱形.
∴BC=AB,
∵$\frac{AE}{AB}$=sinα,
∴BC=AB=$\frac{AE}{sinα}$=$\frac{1}{sinα}$,
∴重叠部分(图中阴影部分)的面积为:BC×AE=$\frac{1}{sinα}$×1=$\frac{1}{sinα}$.
故答案为$\frac{1}{sinα}$.
点评 此题主要考查了菱形的判定与性质,以及三角函数的应用,关键是证明四边形ABCD是菱形,利用三角函数求出BC的长.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
19.以下生活现象中,属于旋转变换得是( )
| A. | 钟表的指针和钟摆的运动 | B. | 站在电梯上的人的运动 | ||
| C. | 坐在火车上睡觉 | D. | 地下水位线逐年下降 |
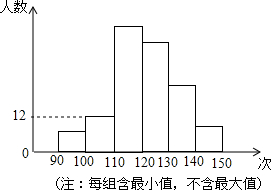 九年级学生进行了中考体育测试,某校抽取了部分学生的一分钟跳绳测试成绩,测试成绩整理后作出如图统计图,甲同学计算出前两组的频率和是0.12,乙同学计算出第一组的频率和为0.04,丙同学计算出从左至右第二、三、四组的频数比为4:17:15,结合统计图回答下列问题
九年级学生进行了中考体育测试,某校抽取了部分学生的一分钟跳绳测试成绩,测试成绩整理后作出如图统计图,甲同学计算出前两组的频率和是0.12,乙同学计算出第一组的频率和为0.04,丙同学计算出从左至右第二、三、四组的频数比为4:17:15,结合统计图回答下列问题