题目内容
(1)如图1,在凹四边形ABCD中,∠BDC=135°,∠B=∠C=30°,则∠A= °.
(2)如图2,在凹四边形ABCD中,∠ABD与∠ACD的角平分线交于点E,∠A=60°,∠BDC=140°,则∠E= °.
(3)如图3,∠ABD,∠BAC的角平分线交于点E,∠C=40°,∠BDC=150°,求∠AEB的度数.
(4)如图4,∠BAC,∠BDC的角平分线交于点E,猜想∠B,∠C与∠E之间有怎样的数量关系,并证明你的猜想.

(2)如图2,在凹四边形ABCD中,∠ABD与∠ACD的角平分线交于点E,∠A=60°,∠BDC=140°,则∠E=
(3)如图3,∠ABD,∠BAC的角平分线交于点E,∠C=40°,∠BDC=150°,求∠AEB的度数.
(4)如图4,∠BAC,∠BDC的角平分线交于点E,猜想∠B,∠C与∠E之间有怎样的数量关系,并证明你的猜想.

考点:三角形的外角性质,三角形内角和定理
专题:
分析:(1)连接AD并延长,根据三角形外角的性质即可得出结论;
(2)连接BC,由三角形内角和定理求出∠ABC+∠ACB的度数,再根据∠BDC=140°求出∠DBC+∠DCB的度数,根据∠ABD与∠ACD的角平分线交于点E求出∠EBD+∠ECD的度数,根据三角形内角和定理即可得出∠E的度数;
(3)延长BD交AC于点F,根据∠BDC是△CDF的外角可求出∠CFD的度数,再根据∠CFD是△ABF的外角可得出∠BAC+∠ABD的度数,进而得出结论;
(4)由(1)可知,∠BAC+∠B+∠C=∠BDC,再由角平分线的定义可知∠BAE=∠CAE=
∠BAC,∠BDE=∠CDE=
∠BDC,由∠1=∠B+∠BAE=∠B+
∠BAC即可得出结论.
(2)连接BC,由三角形内角和定理求出∠ABC+∠ACB的度数,再根据∠BDC=140°求出∠DBC+∠DCB的度数,根据∠ABD与∠ACD的角平分线交于点E求出∠EBD+∠ECD的度数,根据三角形内角和定理即可得出∠E的度数;
(3)延长BD交AC于点F,根据∠BDC是△CDF的外角可求出∠CFD的度数,再根据∠CFD是△ABF的外角可得出∠BAC+∠ABD的度数,进而得出结论;
(4)由(1)可知,∠BAC+∠B+∠C=∠BDC,再由角平分线的定义可知∠BAE=∠CAE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: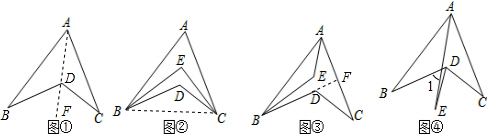 解:(1)连接AD并延长,
解:(1)连接AD并延长,
∵∠BDF是△ABD的外角,∠CDF是△ACD的外角,
∴∠BDF=∠B+∠BAD,∠CDF=∠C+∠CAD,
∴∠BDF+∠CDF=∠B+∠C+∠BAD+∠CAD,即∠BDC=∠B+∠C+∠BAC,
∵∠BDC=135°,∠B=∠C=30°,
∴∠BAC=∠BDC-∠B-∠C=135°-30°-30°=75°.
故答案为:75;
(2)连接BC,
∵∠A=60°,
∴∠ABC+∠ACB=180°-60°=120°,
∵∠BDC=140°,
∴∠DBC+∠DCB=180°-140°=40°,
∴∠ABD+∠ACD=120°-40°=80°,
∵∠ABD与∠ACD的角平分线交于点E,
∴∠EBD+∠ECD=
×80°=40°,
∴∠EBC+∠ECB=40°+40°=80°,
∴∠E=180°-(∠EBC+∠ECB)=180°-80°=100°.
故答案为:100;
(3)延长BD交AC于点F,
∵∠BDC是△CDF的外角,∠C=40°,∠BDC=150°,
∴∠CFD=∠BDC-∠C=150°-40°=110°,
∵∠CFD是△ABF的外角,
∴∠BAC+∠ABD=∠CFD=110°,
∵∠ABD,∠BAC的角平分线交于点E,
∴∠BAE+∠ABE=
(∠BAC+∠ABD)=
×110°=55°,
∴∠AEB=180°-(∠BAE+∠ABE)=180°-55°=125°;
(4)由(1)可知,∠BAC+∠B+∠C=∠BDC,
∵∠BAC,∠BDC的角平分线交于点E,
∴∠BAE=∠CAE=
∠BAC,∠BDE=∠CDE=
∠BDC,
∵∠1=∠B+∠BAE=∠B+
∠BAC,
∴∠B+
∠BAC=∠E+
(∠BAC+∠B+∠C),即∠B-∠C=2∠E.
 解:(1)连接AD并延长,
解:(1)连接AD并延长,∵∠BDF是△ABD的外角,∠CDF是△ACD的外角,
∴∠BDF=∠B+∠BAD,∠CDF=∠C+∠CAD,
∴∠BDF+∠CDF=∠B+∠C+∠BAD+∠CAD,即∠BDC=∠B+∠C+∠BAC,
∵∠BDC=135°,∠B=∠C=30°,
∴∠BAC=∠BDC-∠B-∠C=135°-30°-30°=75°.
故答案为:75;
(2)连接BC,
∵∠A=60°,
∴∠ABC+∠ACB=180°-60°=120°,
∵∠BDC=140°,
∴∠DBC+∠DCB=180°-140°=40°,
∴∠ABD+∠ACD=120°-40°=80°,
∵∠ABD与∠ACD的角平分线交于点E,
∴∠EBD+∠ECD=
| 1 |
| 2 |
∴∠EBC+∠ECB=40°+40°=80°,
∴∠E=180°-(∠EBC+∠ECB)=180°-80°=100°.
故答案为:100;
(3)延长BD交AC于点F,
∵∠BDC是△CDF的外角,∠C=40°,∠BDC=150°,
∴∠CFD=∠BDC-∠C=150°-40°=110°,
∵∠CFD是△ABF的外角,
∴∠BAC+∠ABD=∠CFD=110°,
∵∠ABD,∠BAC的角平分线交于点E,
∴∠BAE+∠ABE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AEB=180°-(∠BAE+∠ABE)=180°-55°=125°;
(4)由(1)可知,∠BAC+∠B+∠C=∠BDC,
∵∠BAC,∠BDC的角平分线交于点E,
∴∠BAE=∠CAE=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠1=∠B+∠BAE=∠B+
| 1 |
| 2 |
∴∠B+
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是三角形外角的性质,熟知三角形的一个外角等于和它不相邻的两个内角的和是解答此题的关键.

练习册系列答案
相关题目
如图是某几何体的三种视图,其表面积为( )


| A、2π | B、3π | C、4π | D、5π |
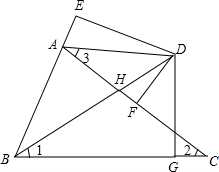 如图,在△ABC中,∠ABC的平分线BD交AC的中垂线DE于D,交AC于H,连接AD,DG⊥BC于G,交AC于K,延长BA至F,使AF=GC,连接DF.
如图,在△ABC中,∠ABC的平分线BD交AC的中垂线DE于D,交AC于H,连接AD,DG⊥BC于G,交AC于K,延长BA至F,使AF=GC,连接DF.
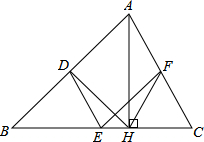 如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.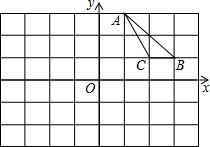 如图,平面直角坐标系中,△ABC的三个顶点A(1,3),B(3,1),C(2,1)
如图,平面直角坐标系中,△ABC的三个顶点A(1,3),B(3,1),C(2,1) 如图,已知DE∥BC,BE平分∠ABNC,∠C=55°,∠ABC=70°.
如图,已知DE∥BC,BE平分∠ABNC,∠C=55°,∠ABC=70°.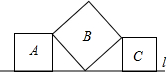 如图,直线l上有三个正方形A,B,C,且正方形A和C的一边在直线l上,正方形B的一个顶点在直线l上,有两个顶点分别与A和C的一个顶点重合,若A和C的面积分别为7和15,则B的面积为
如图,直线l上有三个正方形A,B,C,且正方形A和C的一边在直线l上,正方形B的一个顶点在直线l上,有两个顶点分别与A和C的一个顶点重合,若A和C的面积分别为7和15,则B的面积为