题目内容
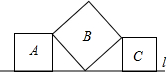 如图,直线l上有三个正方形A,B,C,且正方形A和C的一边在直线l上,正方形B的一个顶点在直线l上,有两个顶点分别与A和C的一个顶点重合,若A和C的面积分别为7和15,则B的面积为
如图,直线l上有三个正方形A,B,C,且正方形A和C的一边在直线l上,正方形B的一个顶点在直线l上,有两个顶点分别与A和C的一个顶点重合,若A和C的面积分别为7和15,则B的面积为考点:全等三角形的判定与性质,勾股定理,正方形的性质
专题:
分析:根据正方形的性质得出∠EFG=∠EGH=∠HMG=90°,EG=GH,求出∠FEG=∠HGM,证△EFG≌△GMH,推出FG=MH,GM=EF,求出EF2=7,HM2=15,求出B的面积为EG=EF2+FG2=EF2+HM2,代入求出即可.
解答:解: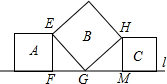
根据正方形的性质得出∠EFG=∠EGH=∠HMG=90°,EG=GH,
∵∠FEG+∠EGF=90°,∠EGF+∠HGM=90°,
∴∠FEG=∠HGM,
在△EFG和△GMH中,
,
∴△EFG≌△GMH(AAS),
∴FG=MH,GM=EF,
∵A和C的面积分别为7和15,
∴EF2=7,HM2=15,
∴B的面积为EG=EF2+FG2=EF2+HM2=7+15=22,
故答案为:22.

根据正方形的性质得出∠EFG=∠EGH=∠HMG=90°,EG=GH,
∵∠FEG+∠EGF=90°,∠EGF+∠HGM=90°,
∴∠FEG=∠HGM,
在△EFG和△GMH中,
|
∴△EFG≌△GMH(AAS),
∴FG=MH,GM=EF,
∵A和C的面积分别为7和15,
∴EF2=7,HM2=15,
∴B的面积为EG=EF2+FG2=EF2+HM2=7+15=22,
故答案为:22.
点评:本题考查了正方形性质,勾股定理,全等三角形的性质和判定的应用,解此题的关键是求出FG=MH,题目比较典型,难度适中.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目

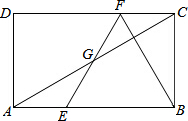 如图,在矩形ABCD中,E、F分别是AB、CD上的点,AE=CF,连接EF、BF,EF交对角线AC于点G,若BE=BF,∠DFE=2∠BAC,BC=
如图,在矩形ABCD中,E、F分别是AB、CD上的点,AE=CF,连接EF、BF,EF交对角线AC于点G,若BE=BF,∠DFE=2∠BAC,BC=
 如图,AB=8,以AB为直径的半圆绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是
如图,AB=8,以AB为直径的半圆绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是