题目内容
11.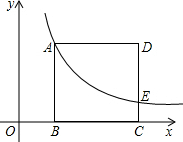 如图,正方形ABCD的顶点B、C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),则k的值为2.
如图,正方形ABCD的顶点B、C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,$\frac{2}{3}$),则k的值为2.
分析 先根据A点坐标得出正方形的边长,再用m表示出n的值,根据反比例函数图象上点的坐标特点得出m、n的方程,求出m、n的值,再求出A点坐标,代入A点坐标即可求得.
解答 解:∵四边形ABCD是正方形,顶点A(m,2),
∴AB=BC=2.
∵E(n,$\frac{2}{3}$),
∴n=2+m①.
∵A、E均在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,
∴2m=$\frac{2}{3}$n②,
①②联立得,m=1,n=3,
∴A(1,2),
∴k=1×2=2.
故答案为2.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
19.若三角形的三边长分别为3,4,x,则x的值可能是( )
| A. | 1 | B. | 6 | C. | 7 | D. | 10 |
 将直角梯形ABCD平移得梯形EFGH,若HG=10,MC=2,MG=4,则图中阴影部分的面积为36.
将直角梯形ABCD平移得梯形EFGH,若HG=10,MC=2,MG=4,则图中阴影部分的面积为36. 已知一次函数y=kx+b的图象与直线y=-$\sqrt{3}$x平行且经过点(2,-$\sqrt{3}$),与x轴、y轴分别交于A,B两点.
已知一次函数y=kx+b的图象与直线y=-$\sqrt{3}$x平行且经过点(2,-$\sqrt{3}$),与x轴、y轴分别交于A,B两点.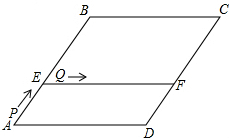 如图,在菱形ABCD中,AB=10,sinA=$\frac{4}{5}$,点E在AB上,AE=4,过点E作EF∥AD,交CD于点F.
如图,在菱形ABCD中,AB=10,sinA=$\frac{4}{5}$,点E在AB上,AE=4,过点E作EF∥AD,交CD于点F.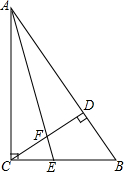 已知,如图,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F,求证:∠CEF=∠CFE.
已知,如图,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F,求证:∠CEF=∠CFE.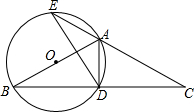 如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE.
如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE.