题目内容
9. 如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示-$\sqrt{2}$,设点B所表示的数为m,则|m+1|+(m+6)的值为( )
如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示-$\sqrt{2}$,设点B所表示的数为m,则|m+1|+(m+6)的值为( )| A. | 3 | B. | 5 | C. | 11-2$\sqrt{2}$ | D. | 9 |
分析 点A表示-$\sqrt{2}$,向右直爬2个单位到达点B,点B表示的数为m=-$\sqrt{2}$+2,判断m的取值范围,对式子进行化简.
解答 解:由题意得,m=-$\sqrt{2}$+2,
所以,|m+1|+(m+6)
=|-$\sqrt{2}$+2+1|+(-$\sqrt{2}$+2+6)
=|-$\sqrt{2}$+3|+(-$\sqrt{2}$+8)
=-$\sqrt{2}$+3-$\sqrt{2}$+8
=11-2$\sqrt{2}$.
故选C.
点评 本题考查了实数与数轴的关系,绝对值的意义.关键是根据题意求出m的值,确定m的范围.

练习册系列答案
相关题目
14.已知函数y=2x2的图象是抛物线,现在同一坐标系中,将该抛物线分别向上、向左平移2个单位,那么所得到的新抛物线的解析式是( )
| A. | y=2(x+2)2+2 | B. | y=2(x+2)2-2 | C. | y=2(x-2)2-2 | D. | y=2(x-2)2+2 |
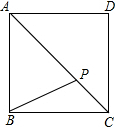 已知点P是正方形ABCD对角线AC上的一点,请探究线段PA,PC,PB的关系式,并写出证明过程.
已知点P是正方形ABCD对角线AC上的一点,请探究线段PA,PC,PB的关系式,并写出证明过程.