��Ŀ����
1������ABCD�ڽ��ڡ�O������ADC��AC���ۣ���D���ڡ�O�ϵ�E��������BE��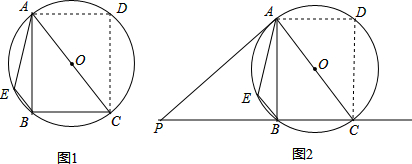
��1����ͼ1���ж��ı���AEBC����״��������֤����
��2����ͼ2��PA�ǡ�O�����߲���CB���ӳ����ڵ�P���е���A������O��ֱ��Ϊ5��$\frac{AB}{PB}=\frac{3}{4}$������M�ӵ�P��������2cm/s���ٶ���������PC�ķ����˶����Ե�MΪԲ�ģ�PM��Ϊ�뾶��Բ�����M�˶���ʱ��Ϊts��t��0����
�ٵ��˶�ʱ��tΪ��ֵʱ����M��ֱ��EB���У�
�ڸ��ݡ�M���߶�AC������ĸ�����ֱ��д����Ӧ���˶�ʱ��t��ֵ��ȡֵ��Χ��
���� ��1����BC=AD=AE��Ѹ�ٵó����ۣ�
��2�������е�ΪG���������е����ʵó�MG��BE��ֱ�����������ƹ�ϵ��ʾ��BM������BM+PM=PC�������̣���֮���ɣ�
�ڷֱ���������ٽ���ʱ�䣺ԲM�պ���AC���У�M��պ���PC�е㴦������PC���е�֮��A��C������ԲM���ˣ�
��� �⣺��1����AE=AD=BC��
�AE=��BC
���ABE=��BAC��
��BE��AC��
��AEBC�ǵ������Σ�
��2������ֱBE��AB���ڵ�F����M��BE�ڵ�G������MG����MG��BE����ͼ2��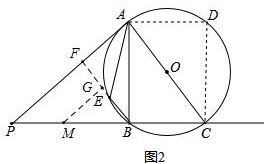
��AP�����ߣ�AC��ֱ����
��AC��AP��
���APB�ס�CPA��
��$\frac{AC}{AP}=\frac{AB}{PB}=\frac{3}{4}$��
��AC=5��
��AP=$\frac{20}{3}$��
��AB=4��PB=$\frac{16}{3}$��BC=3��
�֡ߡ�MGB�ס�ABC��
��$MG=\frac{4}{5}MB$��
��MG=MP=2t��
��MB=$\frac{16}{3}-2t$��
��$2t=\frac{4}{5}����\frac{16}{3}-2t��$��
��ã�t=$\frac{32}{27}$��
����t=$\frac{32}{27}$ʱ����M��ֱ��EB���У�
�ڵ���M��AC�����ڵ�Hʱ����ͼ3��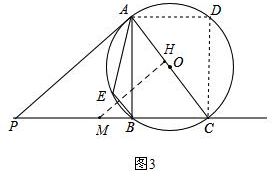
PC=PB+BC=$\frac{25}{3}$��MH=PM=2t��CM=$\frac{25}{3}-2t$��
��$MH=\frac{4}{5}CM$��
��$2t=\frac{4}{5}����\frac{25}{3}-2t��$��
��ã�t=$\frac{50}{27}$��
��MΪPC�е�ʱ��A��Cͬʱ�ڡ�M�ϣ���ʱ��t=$\frac{25}{3}��2��2$=$\frac{25}{12}$��
����������
��0��t��$\frac{50}{27}$ʱ����M��PCû�й����㣻
��t=$\frac{50}{27}$ʱ����M��PC��һ�������㣻
��$\frac{50}{27}$��t��$\frac{25}{12}$ʱ����M��PC�����������㣻
��t��$\frac{25}{12}$ʱ����M��PCû�й����㣮
���� ���⿼���˷��۵����ʡ����ε����ʡ�Բ�����ʡ����ߵ����ʡ����������ε��ж������ʡ�ֱ��������б�����߶����ȶ��֪ʶ�㣬�ۺ��Խ�ǿ����һ���Ѷȣ���ϤԲ�Ļ������ʡ���������˶������е�����λ�á������������������ε��߶α�����ϵ�ǽ����Ĺؼ���

�������ߺ�һ�Ƕ�Ӧ��ȵ�����������ȫ�ȣ�
�����������ߵĴ�ֱƽ�����ཻ��һ�㣻
�������߶�Ӧ��ȵ�����ֱ��������ȫ�ȣ�
��ֱ�߲�����Գ�ͼ�Σ�
| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | 3�� |
| A�� | $\frac{x^6}{x^3}={x^2}$ | B�� | $\frac{x+y}{x+y}=0$ | C�� | $\frac{y+a}{x+a}=\frac{y}{x}$ | D�� | $\frac{-x+y}{x-y}$=-1 |
 ��ͼ��AC��BC��AD��DB�����������У���ʹ��ABC�ա�BAD���Т٢ڢۣ���������ȷ���۵���Ŷ����ں����ϣ�
��ͼ��AC��BC��AD��DB�����������У���ʹ��ABC�ա�BAD���Т٢ڢۣ���������ȷ���۵���Ŷ����ں����ϣ�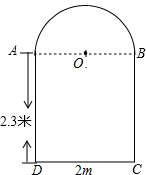 ��ͼ��ijסլ������������¥֮����һ���Ϸ�����ABΪֱ���İ�Բ���·��dz����εķ¹�ͨ������֪AD=2.3�ף�CD=2�ף�����һ������װ���Ҿߺ�2.5�ף���1.6�ף����������ͼҾߵĿ����ܷ�ͨ�����ͨ������˵��������ɣ�
��ͼ��ijסլ������������¥֮����һ���Ϸ�����ABΪֱ���İ�Բ���·��dz����εķ¹�ͨ������֪AD=2.3�ף�CD=2�ף�����һ������װ���Ҿߺ�2.5�ף���1.6�ף����������ͼҾߵĿ����ܷ�ͨ�����ͨ������˵��������ɣ�