题目内容
6.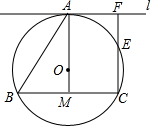 过⊙0上一点A作⊙0的切线l∥弦BC,过C作直线m⊥l于F,交⊙0于点E,
过⊙0上一点A作⊙0的切线l∥弦BC,过C作直线m⊥l于F,交⊙0于点E,(1)试探求线段BC、AF的数量关系;
(2)如果2EF=EC,探讨BC、EC的数量关系;
(3)弧BC的度数是多大范围时,A、E在BC两侧.
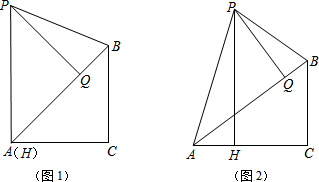
分析 (1)连结AO并延长交BC于M,如图1,利用切线的性质得OA⊥l,再根据平行线的性质得AO⊥BC,则根据垂径定理得BM=CM,再证明四边形AMCF为矩形得到CM=AF,于是得到BC=2AF;
(2)过点O作OH⊥CE于H,连结OC,如图1,根据垂径定理得CH=EH,则利用CE=2EF得到CH=EH=EF,易得OC=OA=CE=2CH=2OM,在Rt△OMC中,利用勾股定理得CM=$\frac{\sqrt{3}}{2}$OC,所以∴BC=$\sqrt{3}$CE;
(3)当OA与BC的垂足点M在半径OA上时,A、E在BC两侧,易得弧BmC的度数.
解答 解:(1)连结AO并延长交BC于M,如图1,
∵l为切线,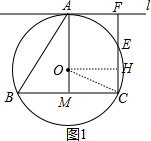
∴OA⊥l,
∵l∥BC,
∴AO⊥BC,
∴BM=CM,
∵CF⊥l,
∴四边形AMCF为矩形,
∴CM=AF,
∴BC=2AF;
(2)过点O作OH⊥CE于H,连结OC,如图1,则CH=EH,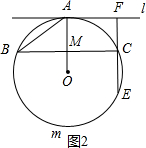
∵CE=2EF,
∴CH=EH=EF,
而OA=FH=2EF=CE,CH=OM,
∴OC=OA=CE=2CH=2OM,
在Rt△OMC中,∵CM=$\sqrt{O{C}^{2}-O{M}^{2}}$=$\sqrt{C{E}^{2}-(\frac{1}{2}CE)^{2}}$=$\frac{\sqrt{3}}{2}$OC,
∴BC=2CM=$\sqrt{3}$OC,
∴BC=$\sqrt{3}$CE;
(3)当弧BmC的度数大于180°小于360°时,A、E在BC两侧,如图2.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.解决(2)小题的关键是构建垂径定理的图形.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
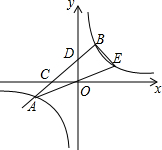 如图,直线AB与双曲线交于点A,B,与x轴,y轴分别交于点C,D,与x轴的夹角α满足tanα=$\frac{3}{4}$,且OD=6,CD:CB=1:2.
如图,直线AB与双曲线交于点A,B,与x轴,y轴分别交于点C,D,与x轴的夹角α满足tanα=$\frac{3}{4}$,且OD=6,CD:CB=1:2.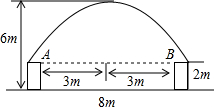 某一隧道内设双行线公路,其截面由一长方形和一抛物线构成,如图所示,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5m,若行车道总宽度AB为6m,请计算车辆经过隧道时的限制高度是多少米?(精确到0.1m)
某一隧道内设双行线公路,其截面由一长方形和一抛物线构成,如图所示,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5m,若行车道总宽度AB为6m,请计算车辆经过隧道时的限制高度是多少米?(精确到0.1m)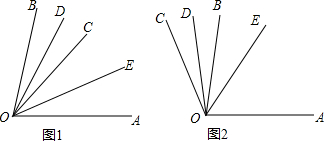 已知:∠AOB=80°,OD、OE分别是∠BOC和∠COA的平分线.
已知:∠AOB=80°,OD、OE分别是∠BOC和∠COA的平分线.