题目内容
12.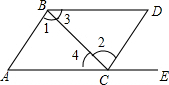 如图所示,点E在AC的延长线上,下列条件中不能判断AC∥BD的是( )
如图所示,点E在AC的延长线上,下列条件中不能判断AC∥BD的是( )| A. | ∠3=∠4 | B. | ∠D=∠DCE | C. | ∠1=∠2 | D. | ∠D+∠ACD=180° |
分析 A、利用内错角相等两直线平行即可得到AC与BD平行;
B、利用内错角相等两直线平行即可得到AC与BD平行;
C、利用内错角相等两直线平行即可得到AB与CD平行;
D、利用同旁内角互补两直线平行即可得到AC与BD平行,
解答 解:A、∵∠3=∠4,∴AC∥BD,故A选项不合题意;
B、∵∠D=∠DCE,∴AC∥BD,故B选项不合题意;
C、∵∠1=∠2,∴AB∥CD,故C选项符合题意;
D、∵∠D+∠ACD=180°,∴AC∥BD,故D选项不符合题意.
故选C.
点评 此题考查了平行线的判定,熟练掌握平行线的判定方法是解本题的关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
11.四边形ABCD中,AC⊥BD,AC≠BD,顺次连接各边中点得到的四边形是( )
| A. | 正方形 | B. | 矩形 | C. | 菱形 | D. | 等腰梯形 |
7.若-1<x<2,则$\sqrt{4-4x+{x}^{2}}$+$\sqrt{{x}^{2}+2x+1}$化简的结果是( )
| A. | -3 | B. | 3 | C. | -2x+1 | D. | 2x-1 |
 如图所示,圆A和圆B的半径都为1,AB=8.圆A和圆B都和圆O外切,且三圆均和直线l相切,切点为C、D、E,则圆O的半径为( )
如图所示,圆A和圆B的半径都为1,AB=8.圆A和圆B都和圆O外切,且三圆均和直线l相切,切点为C、D、E,则圆O的半径为( )
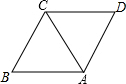 如图,在菱形ABCD中,对角线AC=4,∠B=60°,则菱形ABCD面积为8$\sqrt{3}$.
如图,在菱形ABCD中,对角线AC=4,∠B=60°,则菱形ABCD面积为8$\sqrt{3}$.