题目内容
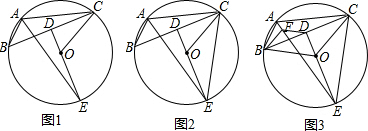
9.已知,△ABC是⊙O的内接三角形,过点O作OD⊥BC于点D,DO交⊙O于点E,连接OC,AE.(1)如图1,求证:∠COE=2∠BAE;
(2)如图2,连接CE,若∠BAC=120°,求证:BC=CE;
(3)如图3,在(2)的条件下,过点B作BF⊥AE于点F,连接FD,若FD=2,AC=6,求DE的长.
分析 (1)根据垂径定理,可得$\widehat{BE}$=$\widehat{CE}$,根据等弧所对的圆周角相等,可得∠BAE=∠CAE,根据圆周角定理,可得∠COE=2∠CAE;
(2)根据等弧所对的圆周角相等,可得∠BAE=∠CAE=∠BCE,∠CBE=∠CAE,根据等边三角形的判定,可得答案;
(3)根据全等三角形的判定与性质,可得AB=AG,FB=FG,根据垂径定理,可得BD与CD的关系,根据三角形中位线的性质,可得CG与FD的关系,根据邻补角的定义,可得∠HAC的度数,根据锐角三角函数,可得CH、AH的长度,根据勾股定理,可得BC的长,再根据锐角三角函数,可得答案.
解答 (1)证明:∵OD⊥BC,$\widehat{BE}$=$\widehat{CE}$,
∴∠BAE=∠CAE.
∵∠COE=2∠CAE,
∴∠COE=2∠BAE;
(2)证明:连接BE. ,
,
∵∠BAE=∠CAE,∠BAC=120°,
∴∠BAE=∠CAE=60°.
∵∠BCE=∠BAE=60°,∠CBE=∠CAE=60°,
∴∠BEC=180°-60°-60°=60°,
∴∠BCE=∠CBE=∠BEC=60°,
∴△BCE是等边三角形,
∴BC=CE;
(3)解:延长BF交AC于G,作CH⊥BA的延长线于H. ,
,
∵BF⊥AE,
∴∠BFA=∠GFA=90°,
在△BAF和△GAF中,
$\left\{\begin{array}{l}{∠BAF=∠GFA}\\{AF=AF}\\{∠BFA=∠GFA}\end{array}\right.$,
∴△BAF≌△GAF (ASA),
∴AB=AG,FB=FG.
∵OD⊥BC,
∴BD=CD.
∵FB=FG,BD=CD,
∴CG=2FD=4,
∴AG=AB=6-4=2.
∵∠HAC=180°°-120°=60°
∴CH=AC•sin60°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,AH=AC•cos60°=6×$\frac{1}{2}$=3,
∴BH=2+3=5,
在Rt△CBH中,BC=$\sqrt{C{H}^{2}+B{H}^{2}}$=$\sqrt{(3\sqrt{3})^{2}+{5}^{2}}$=2$\sqrt{13}$,
∴CD=$\frac{1}{2}$×2$\sqrt{13}$=$\sqrt{13}$,
∵∠ECB=∠EAB=60°,
∴DE=CD•tan60°=$\sqrt{13}$×$\sqrt{3}$=$\sqrt{39}$.
点评 本题考查了圆的综合题,(1)利用了垂径定理,弧与圆周角的关系,圆周角定理;(2)利用了弧与圆周角的关系,等边三角形的判定;(3)利用了全等三角形的判定与性质,三角形中位线定理,锐角三角函数,勾股定理,利用知识点多,题目有一定难度.

 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案| A. |  | B. |  | C. |  | D. |  |
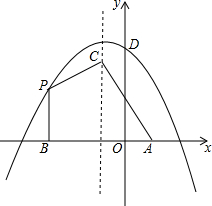 如图,平面直角坐标系中,抛物线y=-$\frac{1}{3}$(x+h)2+k的对称轴为x=-1,与y轴交于点D(0,$\frac{13}{3}$).
如图,平面直角坐标系中,抛物线y=-$\frac{1}{3}$(x+h)2+k的对称轴为x=-1,与y轴交于点D(0,$\frac{13}{3}$).


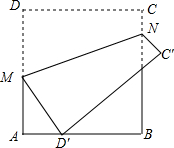 如图,将正方形纸片ABCD沿MN折叠,使点D落在边AB上,对应点为D′,点C落在C′处.若AB=6,AD′=2,则折痕MN的长为2$\sqrt{10}$.
如图,将正方形纸片ABCD沿MN折叠,使点D落在边AB上,对应点为D′,点C落在C′处.若AB=6,AD′=2,则折痕MN的长为2$\sqrt{10}$.