题目内容
17.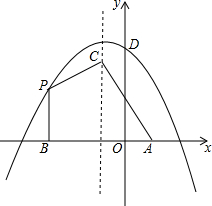 如图,平面直角坐标系中,抛物线y=-$\frac{1}{3}$(x+h)2+k的对称轴为x=-1,与y轴交于点D(0,$\frac{13}{3}$).
如图,平面直角坐标系中,抛物线y=-$\frac{1}{3}$(x+h)2+k的对称轴为x=-1,与y轴交于点D(0,$\frac{13}{3}$).(1)求h和k的值;
(2)点P为第二象限对称轴左侧抛物线上一点,过P作x轴垂线,垂足为B,点B关于抛物线对称轴的对称点为A,在对称轴上取点C,使∠BPC>90°,连接AC,若∠BAC=$\frac{1}{2}$∠BPC.求证:PB=PC;
(3)在(2)条件下,过点A作AE∥PC交抛物线的对称轴于点E,当CE:AE=13:5时,求P点坐标.
分析 (1)根据题意直接求出h的值,进而将D点代入函数解析式求出k的值即可;
(2)连接BC,过P作PH⊥BC于H,进而利用∠BAC=$\frac{1}{2}$∠BPC,得出∠CPH=∠BPH,进而求出△PBH≌△PCH(ASA),得出答案即可;
(3)设对称轴与x轴交于点N,过点P作PQ⊥CE于Q,再证明△PQC≌△ANE(AAS),进而表示出P点坐标,利用图象上点的坐标性质得出P点坐标.
解答 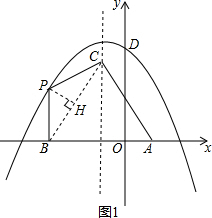 (1)解:∵抛物线的对称轴为:x=-h=-1,
(1)解:∵抛物线的对称轴为:x=-h=-1,
∴h=1,
∴y=-$\frac{1}{3}$(x+1)2+k过D(0,$\frac{13}{3}$),
∴$\frac{13}{3}$=-$\frac{1}{3}$(0+1)2+k,
解得:k=$\frac{14}{3}$;
(2)证明:如图1,连接BC,过P作PH⊥BC于H,
∵B、A关于对称轴对称,
∴CB=CA,∠CBA=∠CAB,
∵PB⊥BA,
∴∠CBA+∠PBC=90°,
∴∠CAB+∠PBC=90°,又∵∠PB+∠BPH=90°,
∴∠CAB=∠BPH,
∵∠BAC=$\frac{1}{2}$∠BPC,
∴∠BPH=$\frac{1}{2}$∠BPC,
∴∠CPH=∠BPH,
在△PBH和△PCH中,
$\left\{\begin{array}{l}{∠BPH=∠CPH}\\{PH=PH}\\{∠BHP=∠PHC}\end{array}\right.$,
∴△PBH≌△PCH(ASA),
∴PB=PC;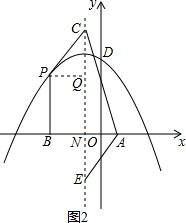
(3)解:如图2,设对称轴与x轴交于点N,过点P作PQ⊥CE于Q,
∵AE∥CP,
∴∠PCQ=∠AEN,PQ=BN=AN,
在△PQC和△ANE中
$\left\{\begin{array}{l}{∠PCQ=∠AEN}\\{∠CQP=∠ENA}\\{PQ=AN}\end{array}\right.$
∴△PQC≌△ANE(AAS),
∴EN=CQ,设CE=13m,则AE=CP=5m,
∴PB=QN=5m,
∴CQ=EN=$\frac{1}{2}$(13m-5m)=4m,
∴PQ=3m,∴P(-3m-1,5m),
代入y=-$\frac{1}{3}$(x+1)2+$\frac{14}{3}$,
5m=-$\frac{1}{3}$(-3m-1+1)2+$\frac{14}{3}$,
解得:m1=$\frac{2}{3}$,m2=-$\frac{7}{3}$(不合题意舍去),
∴P(-3,$\frac{10}{3}$).
点评 此题主要考查了二次函数综合以及全等三角形的判定与性质以及图象上点的坐标性质等知识,熟练应用全等三角形的判定与性质是解题关键.

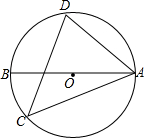 如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=50°,则∠BAD的度数为40°.
如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=50°,则∠BAD的度数为40°.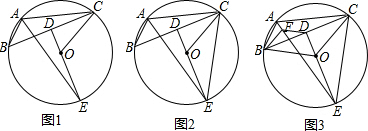
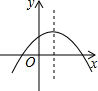 二次函数y=ax2+bx+c的图象在平面直角坐标系中的位置如图所示,则一次函数y=ax+b与反比例函数y=$\frac{c}{x}$在同一平面直角坐标系中的图象可能是( )
二次函数y=ax2+bx+c的图象在平面直角坐标系中的位置如图所示,则一次函数y=ax+b与反比例函数y=$\frac{c}{x}$在同一平面直角坐标系中的图象可能是( )