题目内容
8．
如图，已知点D、E分别在△ABC边AB、AC上，DE∥BC，BD=2AD，那么S△DBE：S△EBC等于（ ）| A． | 1：2 | B． | 1：3 | C． | 1：4 | D． | 2：# |
分析 根据BD=2AD，求出AD：AB的值，在根据相似三角形的性质求得DE：BC，最后再根据面积之比即可求解．
解答 解：∵BD=2AD，
∴AD：AB=1：3，
∵DE∥BC，
∴△ADE∽△ABC，
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$，
∴DE：BC=1：3．
∵△DBE和△EBC的高相同，设这个高为h，
∴S△DBE：S△EBCh=$\frac{\frac{1}{2}DE•h}{\frac{1}{2}BC•h}$=$\frac{DE}{BC}$=$\frac{1}{3}$，
故选B．
点评 本题主要考查了相似三角形的判定和性质，找准对应线段是解题的关键．
练习册系列答案
相关题目
14．（x2y）3的结果是（ ）
| A． | x5y3 | B． | x6y | C． | 3x2y | D． | x6y3 |
如图，在圆内接四边形ABCD中，O为圆心，∠BOD=160°，则∠BCD的度数为100°．
20．若x2-x-m=（x+n）（x+7），则m-n=（ ）
| A． | -64 | B． | -48 | C． | 48 | D． | 64 |
17．
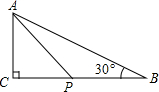如图，△ABC中，∠C=90°，AC=2.5，∠B=30°，点P是BC边上的动点，则AP长不可能是（ ）
如图，△ABC中，∠C=90°，AC=2.5，∠B=30°，点P是BC边上的动点，则AP长不可能是（ ）| A． | 3 | B． | 3.5 | C． | 4.8 | D． | 5.2 |