题目内容
小洁在某超市购买了3盒1L装的牛奶,每盒5.80元,另外又买了12盒250mL装的牛奶,每盒1.50元.
(1)小洁认为她平均每盒花费了
×(5.80+1.50)=3.65(元),对吗?若不对,请写出你认为正确的答案;
(2)其他条件不变,小洁在该超市再购买几盒同样的1L装的牛奶时,使得她平均每盒花费3.65元?
(3)根据(1)(2)的结论,已知数据“a1,a2,…,am;b1,b2,…,bn;c1,c2,…,cp;d1,d2,…,dq每一组数据的平均数分别为a,b,c,d.问当m、n、p、q满足什么条件时,将这四组数据合并为一组:a1,a2,…,am,b1,b2,…,bn,c1,c2,…,cp,d1,d2,…,dq,它的平均数为
(a+b+c+d)?并说明理由.
(1)小洁认为她平均每盒花费了
| 1 |
| 2 |
(2)其他条件不变,小洁在该超市再购买几盒同样的1L装的牛奶时,使得她平均每盒花费3.65元?
(3)根据(1)(2)的结论,已知数据“a1,a2,…,am;b1,b2,…,bn;c1,c2,…,cp;d1,d2,…,dq每一组数据的平均数分别为a,b,c,d.问当m、n、p、q满足什么条件时,将这四组数据合并为一组:a1,a2,…,am,b1,b2,…,bn,c1,c2,…,cp,d1,d2,…,dq,它的平均数为
| 1 |
| 4 |
考点:加权平均数,算术平均数
专题:
分析:(1)用所有牛奶的总钱数除以所有的牛奶的盒数即可求得平均价格;
(2)设小洁购买x盒1L的牛奶时,平均每盒花费3.65元,根据加权平均数的计算公式列出方程即可求解;
(3)根据a1,a2,…,am;b1,b2,…,bn;c1,c2,…,cp;d1,d2,…,dq每一组数据的平均数分别为a,b,c,d得到a1,a2,…,am=am,b1,b2,…,bn=bn,c1,c2,…,cp=cp,d1,d2,…,dq=dq,然后代入加权平均数的计算公式即可求得.
(2)设小洁购买x盒1L的牛奶时,平均每盒花费3.65元,根据加权平均数的计算公式列出方程即可求解;
(3)根据a1,a2,…,am;b1,b2,…,bn;c1,c2,…,cp;d1,d2,…,dq每一组数据的平均数分别为a,b,c,d得到a1,a2,…,am=am,b1,b2,…,bn=bn,c1,c2,…,cp=cp,d1,d2,…,dq=dq,然后代入加权平均数的计算公式即可求得.
解答:解:(1)小洁的说法错误;
正确的为:
=
=2.36元;
(2)设小洁购买x盒1L的牛奶时,平均每盒花费3.65元,
根据题意得:
=3.65,
解得:x=9,
答:小洁在该超市再购买9盒同样的1L装的牛奶时,使得她平均每盒花费3.65元;
(3)当m=n=p=q时,它的平均数为
(a+b+c+d);
理由:∵a1,a2,…,am;b1,b2,…,bn;c1,c2,…,cp;d1,d2,…,dq每一组数据的平均数分别为a,b,c,d,
∴a1,a2,…,am=am,b1,b2,…,bn=bn,c1,c2,…,cp=cp,d1,d2,…,dq=dq,
∵m=n=p=q,
∴平均数为:
=
=
(a+b+c+d).
正确的为:
| 3×5.8+12×1.5 |
| 3+12 |
| 35.4 |
| 15 |
(2)设小洁购买x盒1L的牛奶时,平均每盒花费3.65元,
根据题意得:
| 5.80×(x+3)+1.50×12 |
| x+3+12 |
解得:x=9,
答:小洁在该超市再购买9盒同样的1L装的牛奶时,使得她平均每盒花费3.65元;
(3)当m=n=p=q时,它的平均数为
| 1 |
| 4 |
理由:∵a1,a2,…,am;b1,b2,…,bn;c1,c2,…,cp;d1,d2,…,dq每一组数据的平均数分别为a,b,c,d,
∴a1,a2,…,am=am,b1,b2,…,bn=bn,c1,c2,…,cp=cp,d1,d2,…,dq=dq,
∵m=n=p=q,
∴平均数为:
| am+bn+cp+dq |
| m+n+p+q |
| am+bm+cm+dm |
| m+m+m+m |
| 1 |
| 4 |
点评:本题考查了加权平均数及算术平均数的知识,解题的关键是了解当数据的个数不同时,求平均数不能简单的求两个数据的平均数,难度不大.

练习册系列答案
相关题目
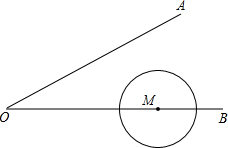 已知:如图所示,∠AOB=30°,M为OB上一点,以M为圆心,5cm为半径作圆,若点M在射线OB上运动,问:
已知:如图所示,∠AOB=30°,M为OB上一点,以M为圆心,5cm为半径作圆,若点M在射线OB上运动,问: