题目内容
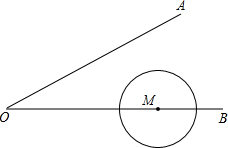 已知:如图所示,∠AOB=30°,M为OB上一点,以M为圆心,5cm为半径作圆,若点M在射线OB上运动,问:
已知:如图所示,∠AOB=30°,M为OB上一点,以M为圆心,5cm为半径作圆,若点M在射线OB上运动,问:(1)当OM满足
(2)当OM满足
(3)当OM满足
考点:直线与圆的位置关系
专题:
分析:根据题意画出圆与直线OA相切是的图形,连接DM,根据∠AOB=30°求出OM的长,再根据直线与圆相交、相离的条件即可得出结论.
解答: 解:如图所示,
解:如图所示,
连接DM,
∵∠AOB=30°,DM=5cm,
∴OM=10cm.
∴当0cm<OM<10cm时,⊙M与OA所在的直线相交;
当OM=10cm时,⊙M与OA所在的直线相切;
当OM>10cm时,⊙M与OA所在的直线相离;
故(1)OM>10cm;(2)OM=10cm;(3)0cm<OM<10cm.
 解:如图所示,
解:如图所示,连接DM,
∵∠AOB=30°,DM=5cm,
∴OM=10cm.
∴当0cm<OM<10cm时,⊙M与OA所在的直线相交;
当OM=10cm时,⊙M与OA所在的直线相切;
当OM>10cm时,⊙M与OA所在的直线相离;
故(1)OM>10cm;(2)OM=10cm;(3)0cm<OM<10cm.
点评:本题考查的是直线与圆的位置关系,熟知设⊙O的半径为r,圆心O到直线l的距离为d.当d<r时,直线l和⊙O相交;当d=r时,直线l和⊙O相切;当d>r时,直线l和⊙O相离是解答此题的关键.

练习册系列答案
相关题目
 直线y=kx+4与y轴交于点A,直线y=-2x+1与直线y=kx+4交于点B与y轴交于点C,点B的横坐标为-1.
直线y=kx+4与y轴交于点A,直线y=-2x+1与直线y=kx+4交于点B与y轴交于点C,点B的横坐标为-1.