题目内容
已知二次函数y=x2+mx+m-5．
（1）求证：不论m取何值时，抛物线总与x轴有两个交点；
（2）求当m取何值时，抛物线与x轴两交点之间的距离最短，最短距离是多少？
（1）求证：不论m取何值时，抛物线总与x轴有两个交点；
（2）求当m取何值时，抛物线与x轴两交点之间的距离最短，最短距离是多少？
考点：抛物线与x轴的交点
专题：
分析：（1）根据b2-4ac与0的大小关系来判断二次函数与x轴交点的个数，即m2-4（m-5）是否大于0，算出其取值范围即可；
（2）设函数与x轴两个交点的值为x1，x2，且x2＞x1，然后可根据函数两个值的和等于-m，两个值的积等于m-5算出x2-x1的值，最后求出其最小值即可．
（2）设函数与x轴两个交点的值为x1，x2，且x2＞x1，然后可根据函数两个值的和等于-m，两个值的积等于m-5算出x2-x1的值，最后求出其最小值即可．
解答：（1）证明：根据b2-4ac与0的大小关系来判断二次函数与x轴交点的个数，
即m2-4×1×（m-5）=m2-4m+20=（m-2）2+16＞0，
所以抛物线总与x轴有两个交点；
（2）解：设函数与x轴两个交点的值为x1，x2，且x2＞x1，
x1+x2=-m，且x1•x2=m-5，
所以（x2-x1）2=（x1+x2）2-4x1x2=m2-4（m-5）=m2-4m+20=（m-2）2+16，
所以当m=2时，x2-x1有最小值4，
所以，抛物线与x轴两交点之间的距离最短为4．
即m2-4×1×（m-5）=m2-4m+20=（m-2）2+16＞0，
所以抛物线总与x轴有两个交点；
（2）解：设函数与x轴两个交点的值为x1，x2，且x2＞x1，
x1+x2=-m，且x1•x2=m-5，
所以（x2-x1）2=（x1+x2）2-4x1x2=m2-4（m-5）=m2-4m+20=（m-2）2+16，
所以当m=2时，x2-x1有最小值4，
所以，抛物线与x轴两交点之间的距离最短为4．
点评：本题主要考查了抛物线与x轴交点和b2-4ac与0的等量关系来判断二次函数与x轴交点的个数以及对于二次函数性质，正确利用完全平方公式是解题关键．．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
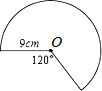如图，从半径为9cm的圆形纸片上剪去圆周的一个扇形，将留下的扇形围成一个圆锥（接缝处不重叠），那么这个圆锥的高为
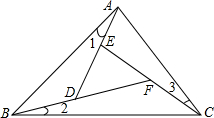在学完三角形的内、外角后，教师要求同学们根据所学的知道设计一个利用“三角形一个外角等于与它不相邻的两个内角的和”求解的问题．
直线y=kx+4与y轴交于点A，直线y=-2x+1与直线y=kx+4交于点B与y轴交于点C，点B的横坐标为-1．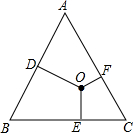
如图三条道路相交围成了一块三角形空地，现要加以绿化，测得AB=BC=AC=115.4米，三角形内的标牌O到三边的距离0F、0D、0E的长度分别为21米、34米、45米，问这块地的面积为多少平方米？