题目内容
4.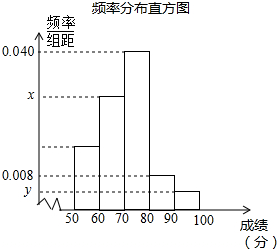 为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计.以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.
为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计.以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图. | 组别 | 分组 | 频数 | 频率 |
| 1 | 50≤x<60 | 9 | 0.18 |
| 2 | 60≤x<70 | a | |
| 3 | 70≤x<80 | 20 | 0.40 |
| 4 | 80≤x<90 | 0.08 | |
| 5 | 90≤x≤100 | 2 | b |
| 合计 |
(1)求出a、b、x、y的值;
(2)老师说:“小王的测试成绩是全班同学成绩的中位数”,那么小王的测试成绩在什么范围内?
(3)若要从小明、小敏等五位成绩优秀的同学中随机选取两位参加竞赛,请用“列表法”或“树状图”求出小明、小敏同时被选中的概率.(注:五位同学请用A、B、C、D、E表示,其中小明为A,小敏为B)
分析 (1)先利用第1组的频数除以它的频率得到样本容量,再计算出第4组的频数,则用样本容量分别减去其它各组的频数得到a的值,接着用第5组的频数除一样本容量得到b的值,用b的值除以组距10得到y的值,然后计算第2组的频率,再把第2组的频率除以组距得到x的值;
(2)根据中位数的定义求解;
(3)画树状图(五位同学请用A、B、C、D、E表示,其中小明为A,小敏为B)展示所有20种等可能的结果数,再找出小明、小敏同时被选中的结果数,然后根据概率公式求解.
解答 解:(1)9÷0.18=50,
50×0.08=4,
所以a=50-9-20-4-2=15,
b=2÷50=0.04,
x=15÷50÷10=0.03,
y=0.04÷10=0.004;
(2)小王的测试成绩在70≤x≤80范围内;
(3)画树状图为:(五位同学请用A、B、C、D、E表示,其中小明为A,小敏为B)
共有20种等可能的结果数,其中小明、小敏同时被选中的结果数为2,
所以小明、小敏同时被选中的概率=$\frac{2}{20}$=$\frac{1}{10}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了统计图.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.如果把分式$\frac{xy}{x+y}$中的x和y都扩大为原来的2倍,那么分式的值( )
| A. | 扩大为原来的4倍 | B. | 扩大为原来的2倍 | C. | 不变 | D. | 缩小为原来的$\frac{1}{2}$ |
3.下列语句中正确的是( )
| A. | 在所有连结两点的线中,直线最短 | |
| B. | ∠AOB与∠BOA表示相同的角 | |
| C. | 一个锐角与一个钝角的和是一个平角 | |
| D. | 两点之间的线段是两点之间的距离 |
1.为了解学生课外阅读的喜好,某校从六年级随机抽取部分学生进行问卷调查,调查要求每人只选取一种喜欢的书籍,如果没有喜欢的书籍,则作“其他”类统计,图(1)与图(2)是整理数据后绘制的两幅不完整的统计图,以下结论不正确的是( )


| A. | 由这两个统计图不能确定喜欢”小说”的人数 | |
| B. | 若该年级共有1200名学生,则可估计喜爱“科普常识”的学生有360人 | |
| C. | 由这两个统计图可知喜好“科普常识”的学生有90人 | |
| D. | 在扇形统计图中,“漫画”所在扇形的圆心角为72° |
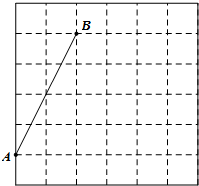 如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.


