题目内容
8．
如图，在△ABC中，BD、CE分别是AC、AB边上的高，求证：B、C、D、E四点在同一个圆上．
分析 取BC的中点F，连接DF、EF，根据直角三角形斜边上的中线等于的一半可得BF=CF=DF=EF，再根据圆的定义证明即可．
解答 
证明：如图，取BC的中点F，连接DF、EF，
∵BD、CE分别是AC、AB边上的高，
∴BF=CF=DF=EF，
∴点B、C、D、E四点在以点F为圆心，以$\frac{1}{2}$BC的半径的圆上，
即B、C、D、E四点在同一个圆上．
点评 本题考查了直角三角形斜边上的中线等于的一半的性质，圆的定义，是基础题，难点在于作辅助线确定出圆的圆心和半径．
练习册系列答案
快捷英语周周练系列答案
相关题目
18．（x-y）2-（x-y）因式分解的结果是（ ）
| A． | （y-x）（x-y） | B． | （x-y）（x-y+1） | C． | （x-y）（x-y-1） | D． | （x-y）（y-x-1） |
19．使分式$\frac{2}{1-3x}$的值为正值的条件是（ ）
| A． | x＜$\frac{1}{3}$ | B． | x＞$\frac{1}{3}$ | C． | x＜0 | D． | x＞0 |
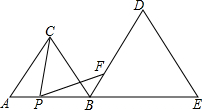等边△ABC和等边△BDE，A、B、E在同-直线上，P是直线AB上一动点，从A向B方向移动．∠CPF=∠A，PF交射线BD于F．
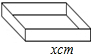如图所示，设长方体底面是边长为xcm的正方形，高为20cm，
20．下列命题中，错误的是（ ）
| A． | 平分弦的直径垂直于弦 | |
| B． | 直径是圆中最长的弦 | |
| C． | 垂直于弦的直径平分弦 | |
| D． | 弦的垂直平分线平分弦所对的两条弧 |
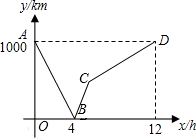一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为x（h），两车之间的距离为y（km），图中的折线表示y与x之间的函数关系．下列说法中正确的是③．