Question

14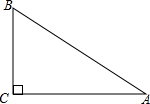．如图，在△ABC中，已知∠C=90°，∠B=60°，BC=2．
（1）求边AB、AC的长；
（2）求△ABC内切圆⊙O的半径r．

Answer 1

分析 （1）利用直角三角形30度角性质，求出AB，再根据勾股定理求出AC即可．
（2）如图，作OE⊥BC于E，OF⊥AC于F，OG⊥AB于G，连接OB、OC、OA，设⊙O半径为r，利用面积法即可解决问题．

解答 解：（1）∵在Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=2，
∴∠CAB=30°，AB=2BC=4，AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=2$\sqrt{3}$，
∴AB=4，AC=2$\sqrt{3}$．

（2）如图，作OE⊥BC于E，OF⊥AC于F，OG⊥AB于G，连接OB、OC、OA，设⊙O半径为r，
∵$\frac{1}{2}$AC•BC=$\frac{1}{2}$BC•OE+$\frac{1}{2}$AC•OF+$\frac{1}{2}$AB•OG，
∴$\frac{1}{2}$×2×2$\sqrt{3}$=$\frac{1}{2}$×（2+4+2$\sqrt{3}$）r，
∴r=$\sqrt{3}$-1．

点评 本题考查三角形内切圆与内心、直角三角形30度角性质等知识，解题的关键是学会利用面积法求内切圆半径，属于中考常考题型．