��Ŀ����
13����ͼ1����ƽ��ֱ������ϵ�У�ֱ��y=$\frac{1}{2}$x-1��������y=-$\frac{1}{4}{x^2}$+bx+c����A��B���㣬��A��x���ϣ���B�ĺ�����Ϊ-8����P��ֱ��AB�Ϸ����������ϵ�һ���㣨�����A��B�غϣ�����1����������ߵĺ�����ϵʽ��
��2������PA��PB���ڵ�P�˶������У��Ƿ����ijһλ�ã�ʹ��PABǡ����һ��ֱ�������Σ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��3����P��PD��y�ύֱ��AB�ڵ�D����PDΪֱ������E�����E��ֱ��AB�Ͻصõ��߶ε���ȣ�
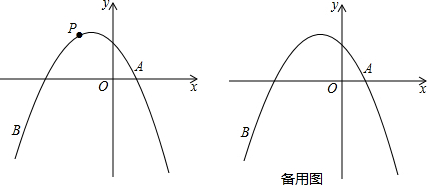
���� ��1������ֱ��y=$\frac{1}{2}$x-1��������y=-$\frac{1}{4}{x^2}$+bx+c����A��B���㣬��A��x���ϣ���B�ĺ�����Ϊ-8�������A��2��0����B��-8��-5�����ô���ϵ������������߽���ʽ��
��2���������������P��ʹ��PABǡ����һ��ֱ�������Σ�ֻ�С�APB=90�㣬��AP��PB�������P�����꣬��ʾ��ֱ��PA��PB�Ľ���ʽ����ֱ��AP��ֱ��PB��б�ʳ˻�����-1�������̣����ɣ�
��3�����жϳ���OCA=��QDF�����ó���AOC�ס�PFD���ó�DF=$\frac{1}{\sqrt{5}}$PD�������DF=PD=$\frac{1}{\sqrt{5}}$����-$\frac{1}{4}$x2-$\frac{3}{2}$x+4�������ɵó����ۣ�
��� ��1���⣺�ߵ�A��x���ϣ���B�ĺ�����Ϊ-8������ֱ��y=$\frac{1}{2}$x-1��
��A��2��0����B��-8��-5����
�ߵ�A��B��������y=-$\frac{1}{4}{x^2}$+bx+c�ϣ�
��0=-1+2b+c��-16-8b+c=-5��
��b=-1��c=3��
�������ߵĽ���ʽΪy=-$\frac{1}{4}{x^2}$-x+3��
��2���⣺�������������P��ʹ��PABǡ����һ��ֱ�������Σ�
�ߡ�PABǡ����һ��ֱ�������Σ�ֱ��y=$\frac{1}{2}$x-1��������y=-$\frac{1}{4}$x 2+bx+c����A��B���㣬PΪ�������ϵĵ�
��ֻ���ǡ�APB=90�㣬��AP��PB
��ֱ��AP��ֱ��PB��б�ʳ˻�����-1
��P��x��-$\frac{1}{4}$x 2-x+3������A������2��0����B������-8��-5����
��$\frac{-{\frac{1}{4}x}^{2}-x+3}{x-2}$��$\frac{-{\frac{1}{4}x}^{2}-x+3+5}{x+8}$=-1��
�ࣨx+6����x-4��=-16��
���x=2���ᣩ��x=-4��
���ڵ�P��-4��3��ʹ��PABǡ����һ��ֱ�������Σ�
��3��
�⣺��OA=2��OC=1��
��AC=$\sqrt{5}$��
��PD��OC��
���OCA=��QDF��
�ߡ�PFD=��AOC=90�㣬
���AOC�ס�PFD��
��$\frac{DF}{PD}$=$\frac{OC}{AC}$=$\frac{1}{\sqrt{5}}$��
��DF=$\frac{1}{\sqrt{5}}$PD��
��D��x��$\frac{1}{2}$x-1����P��x��-$\frac{1}{4}$x2-x+3����
��PD=-$\frac{1}{4}$x2-x+3-$\frac{1}{2}$x+1=-$\frac{1}{4}$x2-$\frac{3}{2}$x+4��
��DF=PD=$\frac{1}{\sqrt{5}}$����-$\frac{1}{4}$x2-$\frac{3}{2}$x+4����
�൱x=-3ʱ��DF���=$\frac{1}{\sqrt{5}}$����-$\frac{1}{4}$��32+$\frac{3}{2}$��3+4��=$\frac{5\sqrt{5}}{4}$��
���� �����Ƕ��κ������ۺ��⣬��Ҫ�����˴���ϵ�����������ߵĽ���ʽ���漰����֪ʶ����Ҫ�У����������ε��ж������ʣ�ƽ������ϵ�л��ഹֱ��ֱ�ߣ�����ϵ���ij˻���-1���жϳ���AOC�ס�PFD�ǽⱾ��Ĺؼ���

 �������ͬ������ϵ�д�
�������ͬ������ϵ�д�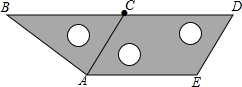 ��ͼ����������ͬ�����ǰ岻�ص�������϶��ƴ��һ�𣬹۲�ͼ�Σ����߶�AB��BD��DE��EC��CA��AE�У��ƽ�е��߶��У�������
��ͼ����������ͬ�����ǰ岻�ص�������϶��ƴ��һ�𣬹۲�ͼ�Σ����߶�AB��BD��DE��EC��CA��AE�У��ƽ�е��߶��У�������| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
| A�� | 9.98��107 | B�� | 9.98��108 | C�� | O��998��109 | D�� | 99.8��107 |
| A�� | -4a2 | B�� | 2a2 | C�� | -2a2 | D�� | 4a2 |
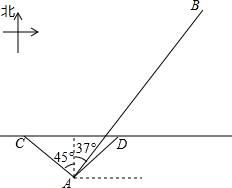 �ҹ��Ϻ�ij������һ���̶�����A��������Ŀ����뾶Ϊ$10\sqrt{2}$���ij�죬�ڵ�A�����������ϵĵ�C����һ���ɴ�ǡ�ý�������������������������ٺ��У��ҷ�������ж�����ߵ繵ͨ�����ɴ�ֻ��2Сʱ��ǡ����D���뿪��������ҷ�����֪ͨ��֪ͨʱ����Բ��ƣ�λ�ڵ�A��ƫ��37�㷽������A���50�����B���ľ��������Ϸ���Կ��ɴ�ֻ����������أ�
�ҹ��Ϻ�ij������һ���̶�����A��������Ŀ����뾶Ϊ$10\sqrt{2}$���ij�죬�ڵ�A�����������ϵĵ�C����һ���ɴ�ǡ�ý�������������������������ٺ��У��ҷ�������ж�����ߵ繵ͨ�����ɴ�ֻ��2Сʱ��ǡ����D���뿪��������ҷ�����֪ͨ��֪ͨʱ����Բ��ƣ�λ�ڵ�A��ƫ��37�㷽������A���50�����B���ľ��������Ϸ���Կ��ɴ�ֻ����������أ� ��ͼ��AB�ǰ�Բ��ֱ������C��D�ǰ�Բ�����㣬��ADC=128�㣬���ABC=52�㣮
��ͼ��AB�ǰ�Բ��ֱ������C��D�ǰ�Բ�����㣬��ADC=128�㣬���ABC=52�㣮