题目内容
16.下列计算正确的是( )| A. | a3+a2=a5 | B. | (a-b)2=a2-b2 | C. | a6b÷a2=a3b | D. | (-ab3)2=a2b6 |
分析 根据合并同类项判定选项A;根据完全平方公式判定选项B;根据单项式的除法法则判定选项C;根据积的乘方法则判定选项D;依此即可求解.
解答 解:A、a3,a2不是同类项,不能合并,故选项错误;
B、(a-b)2=a2-2ab+b2,故选项错误;
C、a6b÷a2=a4b,故选项错误;
D、(-ab3)2=a2b6,故选项正确.
故选:D.
点评 本题考查了整式的混合运算,合并同类项,完全平方公式,单项式的除法以及积的乘方,一定要记准法则和公式才能做题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
6.一水库的水位在最近6天内持续上涨,如表记录了这6天的水位高的:
(1)由记录表推出这6天中水位高度h(m)随时间n(天)变化的函数解析式,并画出函数的图象;
(2)据估计这种上涨的势头还会持续2天,预测再过2天水位高度将达到多少米.
| n(天) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| h(m) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 |
(2)据估计这种上涨的势头还会持续2天,预测再过2天水位高度将达到多少米.
7.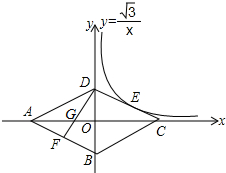 如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF⊥AB交AC于点G,反比例函数y=$\frac{\sqrt{3}}{x}$(x>0)经过线段DC的中点E,若BD=4,则AG的长为( )
如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF⊥AB交AC于点G,反比例函数y=$\frac{\sqrt{3}}{x}$(x>0)经过线段DC的中点E,若BD=4,则AG的长为( )
 如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF⊥AB交AC于点G,反比例函数y=$\frac{\sqrt{3}}{x}$(x>0)经过线段DC的中点E,若BD=4,则AG的长为( )
如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF⊥AB交AC于点G,反比例函数y=$\frac{\sqrt{3}}{x}$(x>0)经过线段DC的中点E,若BD=4,则AG的长为( )| A. | $\frac{4\sqrt{3}}{3}$ | B. | $\sqrt{3}$+2 | C. | 2$\sqrt{3}$+1 | D. | $\frac{3\sqrt{3}}{2}$+1 |
4.当0≤x≤3时,一次函数y=-x+3的最大值是( )
| A. | 0 | B. | 3 | C. | -3 | D. | 无法确定 |
1.计算3x2•(-2x)3的结果是( )
| A. | -18x5 | B. | -24x5 | C. | -24x6 | D. | -18x6 |
5.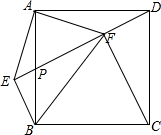 如图,在正方形ABCD中,点P是AB的中点,连接DP,过点B作BE⊥DP的延长线于点E,连接AE,过点A作AF⊥AE,AF交DP于点F,连接BF、CF.下列结论:
如图,在正方形ABCD中,点P是AB的中点,连接DP,过点B作BE⊥DP的延长线于点E,连接AE,过点A作AF⊥AE,AF交DP于点F,连接BF、CF.下列结论:
①△ABE≌△ADF;②FB=AB;③FC=EF;④BF⊥AF;⑤PF=EP+EB.
其中正确的命题个数有( )
 如图,在正方形ABCD中,点P是AB的中点,连接DP,过点B作BE⊥DP的延长线于点E,连接AE,过点A作AF⊥AE,AF交DP于点F,连接BF、CF.下列结论:
如图,在正方形ABCD中,点P是AB的中点,连接DP,过点B作BE⊥DP的延长线于点E,连接AE,过点A作AF⊥AE,AF交DP于点F,连接BF、CF.下列结论:①△ABE≌△ADF;②FB=AB;③FC=EF;④BF⊥AF;⑤PF=EP+EB.
其中正确的命题个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
6.如图图形中,由∠1=∠2能得到AB∥CD的是( )
| A. | 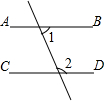 | B. |  | ||
| C. | 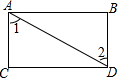 | D. | 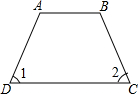 |
 如过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图所示的几何体,其正确的展开图为( )
如过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图所示的几何体,其正确的展开图为( )



 如图,a∥b,一块等腰直角三角板的直角顶点落在直线b上,一个锐角顶点落在直线a上,若∠1=25°,则∠2=65°.
如图,a∥b,一块等腰直角三角板的直角顶点落在直线b上,一个锐角顶点落在直线a上,若∠1=25°,则∠2=65°.