题目内容
求抛物线y=-
x2-x+
的顶点坐标与对称轴,并指出当x取何值时y随x的增大而增大,当x取何值时,y随x的增大而减小.
| 1 |
| 2 |
| 3 |
| 2 |
考点:二次函数的性质
专题:
分析:可通过将二次函数y=-
x2-x+
化为顶点式,再依次判断对称轴、顶点坐标、开口方向及函数增减性等问题.
| 1 |
| 2 |
| 3 |
| 2 |
解答:解:把抛物线y=-
x2-x+
化为顶点坐标式为y=-
x2-x+
=-
(x+1)2+2,
故顶点坐标为(-1,2),对称轴为x=2,
当x<-1时,y随x的增大而增大,当x>-1时,y随x的增大而减小.
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
故顶点坐标为(-1,2),对称轴为x=2,
当x<-1时,y随x的增大而增大,当x>-1时,y随x的增大而减小.
点评:本题主要考查二次函数的性质,解答本题的关键是把抛物线的一般形式转化成顶点坐标式,此题比较简单.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在同一条公路旁,住着五个人,他们在同一家公司上班,如图所示,不妨设这五个人的家分别住在点A,B,D,E,F的位置,公司在点C,若AB=5km,BC=3km,CD=3km,DE=2km,EF=1km,他们全部乘出租车上、下班,车费单位报销,出租车收费标准是:起步价3元(3km以内,包括3km)以后每千米1.5元(不足1km,以1km计算).
在同一条公路旁,住着五个人,他们在同一家公司上班,如图所示,不妨设这五个人的家分别住在点A,B,D,E,F的位置,公司在点C,若AB=5km,BC=3km,CD=3km,DE=2km,EF=1km,他们全部乘出租车上、下班,车费单位报销,出租车收费标准是:起步价3元(3km以内,包括3km)以后每千米1.5元(不足1km,以1km计算).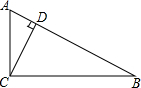 如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D
如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D 在-4,-3,-2,-1,1,2,3,4,m这9个数中,m代表一个数,你认为m是多少时,能够使这9个数分别填入图中的9个空格内,使每行的3个数、每列3个数、斜对角3个数个数相加均为零.
在-4,-3,-2,-1,1,2,3,4,m这9个数中,m代表一个数,你认为m是多少时,能够使这9个数分别填入图中的9个空格内,使每行的3个数、每列3个数、斜对角3个数个数相加均为零.