题目内容
11．
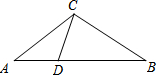如图，△ABC中，点D在AB上，∠ACD=∠ABC，若AD=3，DB=6，求AC的长．
分析 由题意，在△ABC中，点D在边AB上，满足∠ACD=∠ABC，∠A=∠A，可证△ABC∽△ACD，再根据相似三角形对应边成比例来解答即可．
解答 解：∵∠ACD=∠ABC，∠A=∠A，
∴△ACD∽△ABC，
∴$\frac{AD}{AC}$=$\frac{AC}{AB}$，
∵AD=3，AB=6+3=9，
∴$\frac{3}{AC}=\frac{AC}{9}$，
∴AC2=27，
∴AC=3$\sqrt{3}$．
点评 本题主要考查相似三角形的判定和性质，解题的关键在于熟记各种判定方法，难点在于找对应边．
练习册系列答案
小学同步三练核心密卷系列答案
相关题目
如图，在四边形ABCD中，BC、AD不平行，且∠BAD+∠ADC=270°，E、F分别是AD、BC的中点，已知EF=4，求AB2+CD2的值．
如图，Rt△ABC中，AC⊥BC，CD⊥AB于D，AC=8，BC=6，求AD的长．
已知：如图，AD、BC相交于点O，OA=OD，OB=OC，点E、F在AD上，且BE∥CF，