题目内容
19．
如图，Rt△ABC中，AC⊥BC，CD⊥AB于D，AC=8，BC=6，求AD的长．
分析 根据勾股定理求出AB，根据射影定理得到AC2=AD•AB，代入计算即可．
解答 解：∵AC⊥BC，AC=8，BC=6，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10，
∵AC⊥BC，CD⊥AB，
∴AC2=AD•AB，
∴AD=$\frac{A{C}^{2}}{AB}$=6.4．
点评 本题考查的是射影定理和勾股定理的应用，掌握直角三角形中，每一条直角边是这条直角边在斜边上的射影和斜边的比例中项是解题的关键．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
9．
有这样一个问题：探究函数y=$\frac{1}{{{x^2}-1}}$的图象与性质．
小东根据学习函数的经验，对函数y=$\frac{1}{{{x^2}-1}}$的图象与性质进行了探究．下面是小东的探究过程，请补充完成：
（1）自变量取值范围：x≠±1
（2）画图象
①列表
②描点：（见坐标系）
③连线：请你在坐标系中补全图象
（3）进一步探究发现，该函数图象在y轴上有一交点为（0，-1），结合图象，请你写出该函数的其他性质
（一条即可）：x＜-1时y随x增大而增大．
有这样一个问题：探究函数y=$\frac{1}{{{x^2}-1}}$的图象与性质．小东根据学习函数的经验，对函数y=$\frac{1}{{{x^2}-1}}$的图象与性质进行了探究．下面是小东的探究过程，请补充完成：
（1）自变量取值范围：x≠±1
（2）画图象
①列表
| x | … | -$\frac{9}{4}$ | -2 | -$\frac{7}{4}$ | -$\frac{3}{2}$ | -$\frac{5}{4}$ | … |
| y | … | 0.25 | 0.33 | 0.48 | 0.8 | 1.78 | … |
| x | -$\frac{3}{4}$ | -$\frac{1}{2}$ | $\frac{1}{4}$ | 0 | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{3}{4}$ |
| y | -2.29 | -1.33 | -1.07 | -1 | -1.07 | -1.33 | -2.29 |
| x | … | $\frac{5}{4}$ | $\frac{3}{2}$ | $\frac{7}{4}$ | 2 | $\frac{9}{4}$ | … |
| y | … | 1.78 | 0.8 | 0.48 | 0.33 | 0.25 | … |
③连线：请你在坐标系中补全图象
（3）进一步探究发现，该函数图象在y轴上有一交点为（0，-1），结合图象，请你写出该函数的其他性质
（一条即可）：x＜-1时y随x增大而增大．
如图，正方形ABCD，顶点B在直线MN上，AE⊥MN，CF⊥MN，垂足分别为E、F且AE=1，CF=2．求正方形ABCD的面积．
如图，点A，B，C，D在⊙O上，且AB=CD，求证：CE=BE．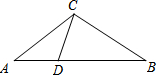
如图，△ABC中，点D在AB上，∠ACD=∠ABC，若AD=3，DB=6，求AC的长．
如图，函数y=-2x和y=kx+b的图象相交于点A（m，3），则关于x的不等式kx+2x+b＞0的解集为x＞-1.5．
9．已知a2+b2=5，a+b=3，则a-b的值为（ ）
| A． | 1 | B． | -2 | C． | ±1 | D． | ±2 |