题目内容
11.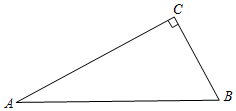 如图,在△ABC中,∠ACB=90°.
如图,在△ABC中,∠ACB=90°.(1)用直尺和圆规过点C作边AB的垂线,交AB于点D(要求:不写作法,保留作图痕迹);
(2)若AC=12,BC=5,求CD的长.
分析 (1)以点C为圆心,以任意长为半径画圆,交BA于点EF,再作EF的垂直平分线即可;
(2)先根据勾股定理求出AB的长,再由三角形的面积公式即可得出结论.
解答 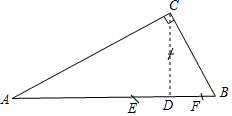 解:(1)如图,线段CD即为所求;
解:(1)如图,线段CD即为所求;
(2)∵在△ABC中,∠ACB=90°,AC=12,BC=5,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{1{2}^{2}+{5}^{2}}$=13,
∴CD=$\frac{AC•BC}{AB}$=$\frac{12×5}{13}$=$\frac{60}{13}$.
点评 本题考查的是作图-基本作图,熟知过直线外一点作已知直线垂线的方法是解答此题的关键.

练习册系列答案
相关题目
1. 如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠AOF的度数是( )
如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠AOF的度数是( )
 如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠AOF的度数是( )
如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠AOF的度数是( )| A. | 130° | B. | 120° | C. | 125° | D. | 100° |
6.下列运算正确的是( )
| A. | (2x2)2=2x2 | B. | x3•x2=x5 | C. | (x3)2=x5 | D. | (x+1)2=x2+1 |
 如图,已知圆内接四边形ABCD,AD是⊙O的直径,OC⊥BD于E.
如图,已知圆内接四边形ABCD,AD是⊙O的直径,OC⊥BD于E. 如图,P是反比例函数y=$\frac{k}{x}$图象上一点,PM∥x轴交y轴于点M,MP=2,点Q的坐标为(4,0),连接PO、PQ,△OPM的面积我3,求该反比例函数的表达式是△OPQ的面积.
如图,P是反比例函数y=$\frac{k}{x}$图象上一点,PM∥x轴交y轴于点M,MP=2,点Q的坐标为(4,0),连接PO、PQ,△OPM的面积我3,求该反比例函数的表达式是△OPQ的面积.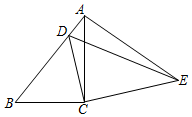 如图,在△ABC中,∠ACB=90°,AB=9,cosB=$\frac{2}{3}$,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,则点A、E之间的距离为4$\sqrt{5}$.
如图,在△ABC中,∠ACB=90°,AB=9,cosB=$\frac{2}{3}$,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,则点A、E之间的距离为4$\sqrt{5}$.