题目内容
9．已知一次函数y=kx-3的图象过点（2，-1），这个函数的解析式为y=x-3．分析 将（2，-1）代入一次函数的解析式即可求出答案．
解答 解：把（2，-1）代入y=kx-3
∴-1=2k-3
∴k=1
∴直线解析式为：y=x-3
故答案为：y=x-3
点评 本题考查待定系数法求解析式，解题的关键是将（2，-1）代入解析式中求出k的值，本题属于基础题型．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
20．为了比较市场上甲乙两种电子钟每日走时误差的情况，从两种电子钟中，各随机抽取10台进行测试，两种电子钟走时误差的数据如表：
（1）计算甲、乙两种电子钟走时误差的平均数；
（2）计算甲、乙两种电子钟走时误差的方差．
| 类型 编号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 |
| 甲种电子钟 | 1 | -3 | -4 | 4 | 2 | -2 | 2 | -1 | -1 | 2 |
| 乙钟电子钟 | 4 | -3 | -1 | 2 | -2 | 1 | -2 | 2 | -2 | 1 |
（2）计算甲、乙两种电子钟走时误差的方差．
17．
为了解国家提倡的“阳光体育运动”的实施情况，将某校中的40名学生一周的体育锻炼时间绘制成了如图所示的条形统计图，根据统计图提供的数据，该校40名同学一周参加体育锻炼时间的众数与中位数分别是（ ）
为了解国家提倡的“阳光体育运动”的实施情况，将某校中的40名学生一周的体育锻炼时间绘制成了如图所示的条形统计图，根据统计图提供的数据，该校40名同学一周参加体育锻炼时间的众数与中位数分别是（ ）| A． | 8，8 | B． | 8，9 | C． | 9，8 | D． | 10，9 |
14．下列各数中，最大的数是（ ）
| A． | -$\frac{1}{2}$ | B． | （-$\frac{1}{2}$）2 | C． | （-$\frac{1}{2}$）3 | D． | （-$\frac{1}{2}$）4 |
1．表反映了平面内直线条数与它们最多交点个数的对应关系：
按此规律，6条直线相交，最多有个交点；n条直线相交，最多有$\frac{n（n+1）}{2}$个交点．（n为正整数）
| 图形 |  |  |  | … |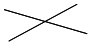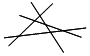
| 直线条数 | 2 | 3 | 4 | … |
| 最多交点个数 | 1 | 3=1+2 | 6=1+2+3 | … |
如图，∠MON=30°，且OP平分∠MON，过点P作PQ∥OM交ON于点Q．若点P到OM的距离为2，则OQ的长为（ ）