题目内容
20.某总公司为了评价甲、乙两个分公司去年的产值,统计了这两个分公司去年12个月的产值(单位:万元)情况,分别如图所示: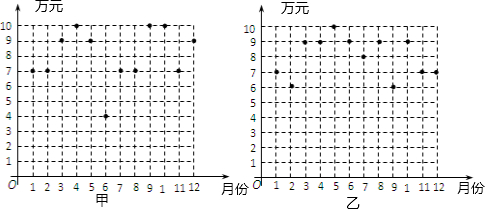
(1)利用上图中的信息,完成下表:
| 平均数 | 中位数 | 众数 | 方差 | |
| 甲 | 8 | 8 | 7 | 3 |
| 乙 | 8 | 8.5 | 9 | 1.5 |
①从平均数和众数相结合看(分析哪个公司产值好些);
②从平均数和中位数相结合看(分析哪个公司产值好些).
③从平均数和方差相结合看(分析哪个公司产值好些).
分析 (1)根据众数和中位数的定义即可得;
(2)根据平均数、众数、中位数及方差的意义逐一分析判断.
解答 解:(1)由图甲知7出现次数最多,有5次,故甲的众数为7;
由图乙知,这12个数据为:6、6、7、7、7、8、9、9、9、9、9、10,
则乙的中位数为$\frac{8+9}{2}$=8.5,
补全表格如下:
| 平均数 | 中位数 | 众数 | 方差 | |
| 甲 | 8 | 8 | 7 | 3 |
| 乙 | 8 | 8.5 | 9 | 1.5 |
∴乙公司的产值好一些;
②∵平均数都相同,乙公司的中位数较小,
∴乙公司的产值好些.
③∵平均数都相同,乙公司的方差较小,
∴乙公司的产值稳定,故乙公司产值好些.
点评 本题考查平均数,众数和中位数的定义:一组数据的中位数与这组数据的排序及数据个数有关,因此求一组数据的中位数时,先将该组数据按从小到大(或按从大到小)的顺序排列,然后根据数据的个数确定中位数:当数据个数为奇数时,则中间的一个数即为这组数据的中位数;当数据个数为偶数时,则最中间的两个数的算术平均数即为这组数据的中位数.

练习册系列答案
相关题目
5.已知p,q是方程x2-3x-1=0的两根,且p>q,则p2-q2的值是( )
| A. | $\sqrt{13}$ | B. | -$\sqrt{13}$ | C. | 3$\sqrt{13}$ | D. | -3$\sqrt{13}$ |
 如图,△ABC的三条中线AD、BE、CF交于点O,请找出图中所有面积相等的三角形.
如图,△ABC的三条中线AD、BE、CF交于点O,请找出图中所有面积相等的三角形.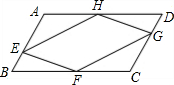 如图,在?ABCD中,AE=CG,BF=DH,连接EF,FG,GH,HE.求证:四边形EFGH是平行四边形.
如图,在?ABCD中,AE=CG,BF=DH,连接EF,FG,GH,HE.求证:四边形EFGH是平行四边形.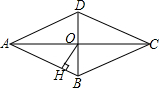 如图,菱形ABCD的对角线AC、BD相交于点O,且AC=8,BD=6,过点O作OH丄AB,垂足为H,则菱形的面积为24,点O到边AB的距离OH=2.4.
如图,菱形ABCD的对角线AC、BD相交于点O,且AC=8,BD=6,过点O作OH丄AB,垂足为H,则菱形的面积为24,点O到边AB的距离OH=2.4.