题目内容
1.如图,菱形ABCD的边长为4cm,∠B=60°,CE⊥AB于E,动点P从出发点以1cm/s的速度沿BC边向终点C运动,同时动点Q从点C出发以4cm/s的速度沿CD边向点D运动,当点Q到达D时立即以原来的速度沿射线DA运动,连接PQ,当点P到达C点时,点P、点Q同时停止运动,设点P,Q运动时间为t秒.(1)当t=1s时,点Q到达点D;
(2)如图1,当点Q在CD上运动时,若△PCQ的面积等于△BEC的面积,求t的值;
(3)如图2,当点Q在DA的延长线上运动时,PQ与AB相交于点F,若AF:BF=3:2,求t的值,并判断此时PQ与CE的位置关系;
(4)在整个运动过程中,是否存在将菱形ABCD的周长和面积同时平分的情形?若存在,请直接写出t的值;若不存在,简要说明理由.

分析 (1)根据时间=$\frac{路程}{速度}$即可求解;
(2)首先求得△BCE的面积,然后利用t表示出PC和CQ的长,则△PCQ的面积即可用t表示,则列方程即可求解;
(3)易证△AQF∽△BPF,根绝相似三角形的对应边的比相等即可列方程求解;
(4)PQ同时把菱形ABCD的周长和面积同时平分,则PQ一定经过菱形的中心,则一定有DQ=BP,据此即可求解.
解答 解:(1)t=$\frac{4}{4}$=1(s),故答案是:1s;
(2)在直角△BCE中,EC=BC•sin∠B=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$(cm),BE=$\frac{1}{2}$BC=2(cm),
则S△BEC=$\frac{1}{2}$BE•EC=$\frac{1}{2}$×2$\sqrt{3}$×2=2$\sqrt{3}$(cm2),
运动的时间是ts,则BP=t,PC=4-t,CQ=4t,
则S△PCQ=$\frac{1}{2}$PC•CQ•sin60°=$\frac{1}{2}$(4-t)•4t•$\frac{\sqrt{3}}{2}$=-t2+4t,
则-t2+4t=2$\sqrt{3}$,
解得:t=1或$\frac{3}{2}$(舍去).
故t=1.
(3)∵AD∥BC,
∴△AQF∽△BPF,
∴$\frac{AQ}{BP}$=$\frac{AF}{BF}$=$\frac{3}{2}$,
∴$\frac{4t-8}{t}$=$\frac{3}{2}$,
解得:t=$\frac{16}{5}$.
则BP=$\frac{16}{5}$,
又∵BF=$\frac{2}{5}$AB=$\frac{8}{5}$,BE=2,
∴$\frac{BP}{BC}$=$\frac{BF}{BE}$,
∴PQ∥CE;
(4)PQ同时把菱形ABCD的周长和面积同时平分,则PQ一定经过菱形的中心,
则Q在AD上,且DQ=BP,则t-4=t,
此时无解,则t不存在.
点评 本题考查了相似三角形的判定与性质以及三角函数的应用,正确利用相似三角形的性质求得BP的长是关键.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
| A. | sinB=$\frac{3}{5}$ | B. | cosB=$\frac{3}{4}$ | C. | tanB=$\frac{4}{3}$ | D. | cotB=$\frac{3}{4}$ |
| A. | 4 | B. | 1 | C. | -2 | D. | -5 |
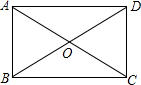 如图,在矩形ABCD中,AB=2,∠AOB=60°,则OB的长为( )
如图,在矩形ABCD中,AB=2,∠AOB=60°,则OB的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 古代有一位商人有一块三角形土地,土地的一边靠水渠,如图所示,现在他想把这块土地平均分给他的三个儿子,为使土地灌溉方便,想使每个儿子分得的土地都有一边和水渠相邻,试问应如何分割这块土地,请说明理由.
古代有一位商人有一块三角形土地,土地的一边靠水渠,如图所示,现在他想把这块土地平均分给他的三个儿子,为使土地灌溉方便,想使每个儿子分得的土地都有一边和水渠相邻,试问应如何分割这块土地,请说明理由. | A. | 精确到万位 | B. | 精确到百分位 | C. | 精确到千分位 | D. | 精确到十分位 |
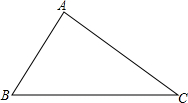 如图,已知△ABC,请你把它分成面积相等的四个小三角形,你能想出几种方法?
如图,已知△ABC,请你把它分成面积相等的四个小三角形,你能想出几种方法?