题目内容
3．
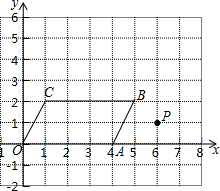在平面直角坐标系内有一平行四边形点O（0，0），A（4，0），B（5，2），C（1，2），有一次函数y=kx+b的图象过点P（6，1）．（1）若此一次函数图象经过平行四边形OA边的中点，求k的值；
（2）若此一次函数图象与平行四边形OABC始终有两个交点，请求出k的取值范围．
分析 （1）设OA的中点为M，根据M、P两点的坐标，运用待定系数法求得k的值；
（2）当一次函数y=kx+b的图象过B、P两点时，求得k的值；当一次函数y=kx+b的图象过A、P两点时，求得k的值，最后判断k的取值范围．
解答 解：（1）设OA的中点为M，
∵O（0，0），A（4，0），
∴OA=4，
∴OM=2，
∴M（2，0），
∵一次函数y=kx+b的图象过M、P两点，
∴$\left\{\begin{array}{l}6k+b=1\\ 2k+b=0\end{array}\right.$，
解得：$k=\frac{1}{4}$；
（2）如图，当一次函数y=kx+b的图象过B、P两点时，
代入表达式y=kx+b得到：
$\left\{\begin{array}{l}6k+b=1\\ 5k+b=2\end{array}\right.$，
解得：k=-1，
当一次函数y=kx+b的图象过A、P两点时，
代入表达式y=kx+b得到：
$\left\{\begin{array}{l}6k+b=1\\ 4k+b=0\end{array}\right.$，
解得：$k=\frac{1}{2}$，
所以$-1＜k＜\frac{1}{2}$，
由于要满足一次函数的存在性，
所以$-1＜k＜\frac{1}{2}$，且k≠0．
点评 本题主要考查了运用待定系数法求一次函数解析式，解题时注意：求正比例函数y=kx，只要一对x，y的值；而求一次函数y=kx+b，则需要两组x，y的值．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
端午节假期间，小亮一家到某度假村度假．小亮和他妈妈坐公交车先出发，他爸爸自驾车沿着相同的道路后出发．他爸爸到达度假村后，发现忘了东西在家里，于是立即返回家里取，取到东西后又马上驾车前往度假村．如图是他们离家的距离s（km）与小明离家的时问t（h）的关系图．请根据图回答下列问题：
李老师准备网上在线学习，现有甲、乙两家网站供李老师选择，已知甲网站的收费方式是：月使用费7元，包时上网时间25小时，超时费每分钟0.01元； 乙网站的月收费方式如图所示．设李老师每月上网的时间为x小时，甲、乙两家网站的月收费金额分别是y1、y2．
如图，一次函数$y=-\frac{2}{3}x+2$的图象分别与x轴、y轴交于A、B，已线段AB为边在第一象限内作等腰Rt△ABC，使∠BAC=90°．
如图，在△ABC中，D是BC边的中点，F，E分别是AD及其延长线上的点，CF∥BE，连结BF，CE．