题目内容
14.四张扑克牌(方块2、黑桃4、黑桃5、梅花5)的牌面如图l,将扑克牌洗匀后,如图2背面朝上放置在桌面上.小亮和小明设计的游戏规则是两人同时抽取一张扑克牌,两张牌面数字之和为奇数时,小亮获胜;否则小明获胜.请问这个游戏规则公平吗?并说明理由.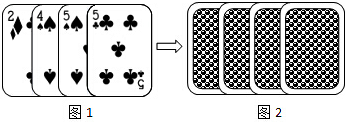
分析 先利用树状图展示所有有12种等可能的结果,其中两张牌面数字之和为奇数的有8种情况,再根据概率公式求出P(小亮获胜)和P(小明获胜),然后通过比较两概率的大小判断游戏的公平性.
解答 解:此游戏规则不公平.
理由如下:
画树状图得:
共有12种等可能的结果,其中两张牌面数字之和为奇数的有8种情况,
所以P(小亮获胜)=$\frac{8}{12}$=$\frac{2}{3}$;P(小明获胜)=1-$\frac{2}{3}$=$\frac{1}{3}$,
因为$\frac{2}{3}$>$\frac{1}{3}$,
所以这个游戏规则不公平.
点评 本题考查了游戏公平性:判断游戏公平性需要先计算每个事件的概率,然后比较概率的大小,概率相等就公平,否则就不公平.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
4.要使分式$\frac{x-1}{x-2}$有意义,则x的取值应满足( )
| A. | x≠2 | B. | x≠1 | C. | x=2 | D. | x=1 |
9.直径为0.00000008米,用科学记数法表示为( )米.
| A. | 0.8×10-7 | B. | 8×10-8 | C. | 8×10-9 | D. | 8×10-7 |
17.已知等腰三角形的底边长为10,腰长为13,则一腰上的高为( )
| A. | 12 | B. | $\frac{60}{13}$ | C. | $\frac{120}{13}$ | D. | $\frac{13}{5}$ |