题目内容
在等边△ABC、△CDE中，AB=6，CD=2，点D在边BC的延长线上，线段AE的长为 ．
考点：等边三角形的性质
专题：分类讨论
分析：根据已知画出符合题意的图形，进而利用勾股定理得出AE的长．
解答：
解：如图1，延长CE，作AF⊥CE交于点F，
∵等边△ABC、△CDE中，
∴∠BCA=∠ACE=∠DCE=60°，
∴∠FAC=30°，
∴CF=
AC=3，
∵EC=2，
∴EF=1，
∵在Rt△ACF中，
∴AF=
=3
，
∵在Rt△AEF中，
∴AE=
=2
，
如图2，当A、C、E在一条直线上，AE=AC+CE=8，
故线段AE的长为8或2
．
故答案为：8或2
．
解：如图1，延长CE，作AF⊥CE交于点F，∵等边△ABC、△CDE中，
∴∠BCA=∠ACE=∠DCE=60°，
∴∠FAC=30°，
∴CF=
| 1 |
| 2 |
∵EC=2，
∴EF=1，
∵在Rt△ACF中，
∴AF=
| AC2-FC2 |
| 3 |
∵在Rt△AEF中，
∴AE=
| AF2+EF2 |
| 7 |
如图2，当A、C、E在一条直线上，AE=AC+CE=8，
故线段AE的长为8或2
| 7 |
故答案为：8或2
| 7 |
点评：此题主要考查了等边三角形的性质以及勾股定理等知识，利用分类讨论得出符合题意的图形是解题关键．
练习册系列答案
相关题目
如图，一块六边形绿化园地，六角都做有半径为R的圆形喷水池，则这六个喷水池占去的绿化园地的面积为
如图，将边长都为2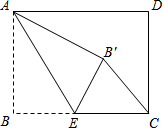
如图，矩形ABCD中，AB=6，BC=8，点E是BC边上一点，连接AE，把∠B沿AE折叠，使点B落在点B′处，当△CEB′为直角三角形时，BE的长为