题目内容
 如图,将边长都为2
如图,将边长都为2| 2 |
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:标注字母,过点A1作A1D、A1E与正方形的边垂直,根据正方形的性质可得A1D=A1E,再求出∠BA1D=∠CA1E,然后利用“角边角”证明△A1BD和△A1CE全等,然后根据全等三角形的性质可得阴影部分的面积等于正方形面积的
,再根据重叠部分的个数比正方形的个数少1进行计算即可得解.
| 1 |
| 4 |
解答: 解:如图,过点A1作A1D、A1E与正方形的边垂直,
解:如图,过点A1作A1D、A1E与正方形的边垂直,
∵A1是正方形的中心,
∴A1D=A1E,A1D⊥A1E,
∵∠BA1D+∠BA1E=∠CA1E+∠BA1E,
∴∠BA1D=∠CA1E,
在△A1BD和△A1CE中,
,
∴△A1BD≌△A1CE(SAS),
∴阴影部分的面积=正方形面积的
=
×(2
)2=2,
∴2014个这样的正方形重叠部分的面积和=2×(2014-1)=4026.
故答案为:4026.
 解:如图,过点A1作A1D、A1E与正方形的边垂直,
解:如图,过点A1作A1D、A1E与正方形的边垂直,∵A1是正方形的中心,
∴A1D=A1E,A1D⊥A1E,
∵∠BA1D+∠BA1E=∠CA1E+∠BA1E,
∴∠BA1D=∠CA1E,
在△A1BD和△A1CE中,
|
∴△A1BD≌△A1CE(SAS),
∴阴影部分的面积=正方形面积的
| 1 |
| 4 |
| 1 |
| 4 |
| 2 |
∴2014个这样的正方形重叠部分的面积和=2×(2014-1)=4026.
故答案为:4026.
点评:本题考查了正方形的性质,全等三角形的判定与性质,作辅助线构造出全等三角形并求出阴影部分的面积等于正方形面积的
是解题的关键,要注意阴影部分的个数比正方形的个数少1.
| 1 |
| 4 |

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
 如图,矩形ABCD中,AB=5cm,BC=10cm,动点M从点D出发,按折线DCBAD方向以3cm/s的速度运动,动点N从点D出发,按折线DABCD方向以2cm/s的速度运动.点E在线段BC上,且BE=1cm,若M、N两点同时从点D出发,到第一次相遇时停止运动.
如图,矩形ABCD中,AB=5cm,BC=10cm,动点M从点D出发,按折线DCBAD方向以3cm/s的速度运动,动点N从点D出发,按折线DABCD方向以2cm/s的速度运动.点E在线段BC上,且BE=1cm,若M、N两点同时从点D出发,到第一次相遇时停止运动.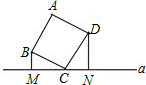 如图,正方形ABCD的顶点C在直线a上,且点B,D到a的距离分别是1,2.则这个正方形的边长是
如图,正方形ABCD的顶点C在直线a上,且点B,D到a的距离分别是1,2.则这个正方形的边长是