题目内容
对于二次函数y=-2(x+1)2+1,下列说法正确的是( )
| A、图象开口向上 |
| B、对称轴是直线x=1 |
| C、顶点坐标是(1,1) |
| D、函数y有最大值,且最大值是1 |
考点:二次函数的性质
专题:
分析:根据二次函数的性质对各选项进行判断.
解答:解:二次函数y=-2(x+1)2+1的图象的开口向下,对称轴为直线x=-1,顶点坐标为(-1,1),函数有最大值1.
故选D.
故选D.
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
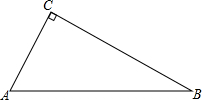 如图所示,在直角三角形ABC中,∠C=90°,AC=6,BC=8,将△ABC绕点B旋转90°,得到关于点A的对称点D,则AD的长是( )
如图所示,在直角三角形ABC中,∠C=90°,AC=6,BC=8,将△ABC绕点B旋转90°,得到关于点A的对称点D,则AD的长是( )| A、20 | ||
| B、10 | ||
C、10
| ||
D、20
|
 如图①,图②,图③…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第20个“广”字中的棋子个数是( )
如图①,图②,图③…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第20个“广”字中的棋子个数是( )| A、43 | B、44 | C、45 | D、46 |
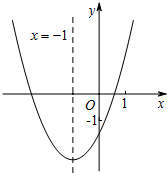 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=-1,与x轴的交点为(x1,0)、(x2,0),其中0<x1<1,有下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=-1,与x轴的交点为(x1,0)、(x2,0),其中0<x1<1,有下列结论:其中,正确的结论有( )
①abc>0;②-3<x2<-2;③4a+1>2b-c;④4ac-b2+4a<0;⑤a>
| 1 |
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
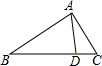 如图,点D是△ABC的边BC上一点,能判断△ACD∽BCA的条件是( )
如图,点D是△ABC的边BC上一点,能判断△ACD∽BCA的条件是( )| A、AC2=BC•DC |
| B、AC•AD=BC•AB |
| C、∠CAD=∠BAD |
| D、∠C=∠B |

 已知∠3+∠2=180°,∠1=45°,求∠4的度数.
已知∠3+∠2=180°,∠1=45°,求∠4的度数.